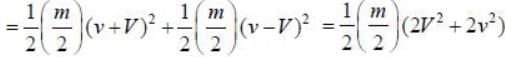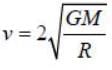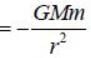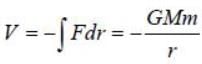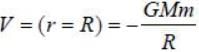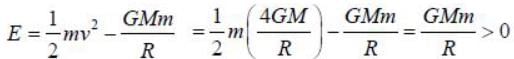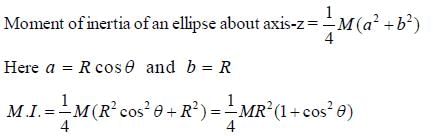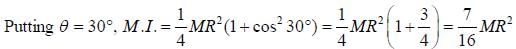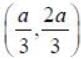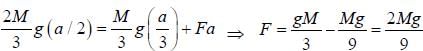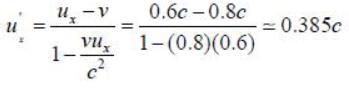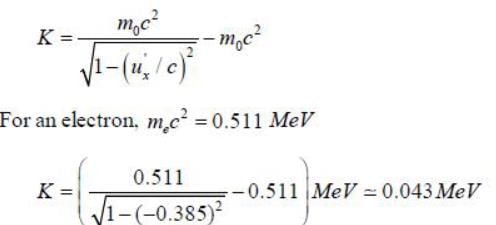Test: Combined (CM+MP) - Physics MCQ
30 Questions MCQ Test GATE Physics Mock Test Series 2026 - Test: Combined (CM+MP)
Consider a particle of mass m moving in a one dimension under a force with the potential V ( x ) = a |x3 - 3xl). where the constant k > 0. The frequency of a small amplitude oscillation of the panicle about the equilibrium position
If the functions G and F depends on the position co-ordinates qi momenta pi and time t, then poisson bracket of G and F is defined as
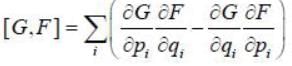
Then [G,pr] (Here r is arbitrary number)
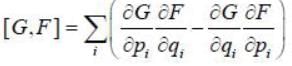
Then [G,pr] (Here r is arbitrary number)
Two forces are given below in spherical polar and cartersian coordiantes

Where A, B and R are constants. Then

Where A, B and R are constants. Then
The Lagrangian of a particle is
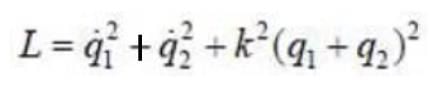
where k is a positive constant, q1 and q2 in generalised coordinates. The equation of motion are
Let (p.q) and (P, Q) be two pairs of canonical variables. The transformation P -q cot βp and 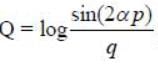 is canonical for β = nα. The value of n is_______
is canonical for β = nα. The value of n is_______
The mass of a particle is measured to be √2 times of its rest mass. The ratio of kinetic energy and total energy is ____________ (up to two decimal places)
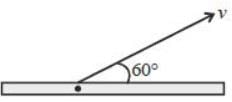
The percentage contraction of a rod moving with a velocity 0.8 c in a direction inclined at 60° to its own length ______% (up to one decimal place)
The Hamiltonian of a particle with mass m =1/2 units moving along x-axis inside a potential V(x) = ex is given by H = p2 + ex Assume p> 0. The phase space trajectory of the particle will be
In a central force field, the trajecting (in plane polar co-oridantes) of a particle is given by  where m is the mass of the particle. L is angular momentiun and e is the eccentricity of the particle's motion. Whcih one of the following conditions given rise to circular trajectory?
where m is the mass of the particle. L is angular momentiun and e is the eccentricity of the particle's motion. Whcih one of the following conditions given rise to circular trajectory?
The minimum value of coefficient of friction for an inclined plane of angle θ = 450 in order that a hoop will roll down without slipping is______(Upto one decimal place)
A distant galaxy is observed to have its hydrogen- β line shifted to a wavelength of 580 nm, away from the laboratory value of 434 mn. The approximate velocity of recession of the distant galaxy is
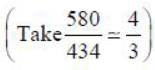
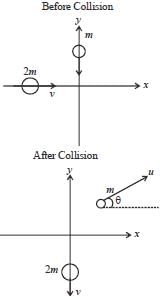
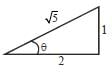
Two balls, of mass m and mass 2m. approach from perpendicular directions with identical speeds and collide. After the collision, the more massive ball moves with the same speed v but downward, perpendicular to its original direction. The less massive ball moves with speed U at an angle θ with respect to the horizontal. If no external forces act during the collision then the final speed of less massive ball is αv. The value of α is_______ (up to 1 decimal place)
The orthogonal trajectories to the curve x2 + (y-1)2 = 1 are a family of
Consider a charged sphere of radius R with charge density f(r ) = e-r. The gradient vector to the family of equipotential surfaces of this charged surface points
The value of the integral 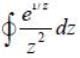 over a contour of unit circle centered at origin. (Taken in the anticlockwise sense) is_______(Answer should be an integer)
over a contour of unit circle centered at origin. (Taken in the anticlockwise sense) is_______(Answer should be an integer)
Given 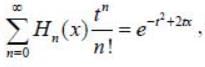 the value of H5(0 ) is _________ (Answer should be an integer)
the value of H5(0 ) is _________ (Answer should be an integer)
Which one of the following combinations can be a possible set of eigenvalues for a 4 x 4 unitary matrix?
Consider a complex function f(x. y) = eax + i In by. If the function is analytic at (0. 1) then the possible values of (a, b) is
If δ(x) is the Dirac-Delta function. and x has the dimension of angular momentum, then δ(x) has a dimension which can be written as [LαMβTy]. The value of (α,β,γ) is
The value of Trace 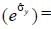 ______ where
______ where 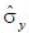 is the pauli matrix
is the pauli matrix 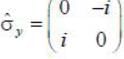 (upto 2 decimal places)
(upto 2 decimal places)
Consider a vector 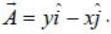 The line integral
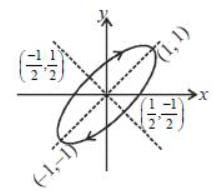
The line integral  over the contour as shown is equal to _____ (upto 2 decimal places)
over the contour as shown is equal to _____ (upto 2 decimal places)
Given below are forces in Cartesian and spherical coordinates. Which of the following are conservative?
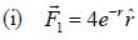
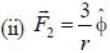

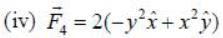
A particle of m moves with speed v. Ail explosion divides the particle into two half, giving each half a speed V in the centre of mass frame. Assume all motion is confined to one dimension. The increase in kinetic energy in the Lab frame is
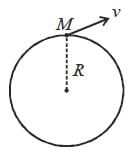
A particle is thrown from earth's surface with speed 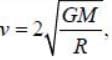 where M and R are mass and radius of the earth respectively. The trajectory of the particle will be a /an
where M and R are mass and radius of the earth respectively. The trajectory of the particle will be a /an
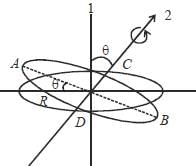
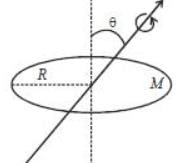
A cricular disc is rotaing about an axis, shown in figure, makes an angle θ = 300 with the vertical axis. The moment of inertia of the disc about that axis is
A block of mass M with the shape of an inverted trapezoid is pushed downwards minimum force required to tip the block is

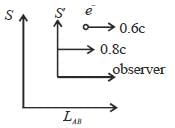
An electron moves in the lab with a speed of 0.6c. An observer moves with a velocity of 0.8 c along the direction of the motion of the electron. The kinetic energy of the electron as determined by the observer is _____ MeV (Upto three decimal places)
|
1 docs|34 tests
|


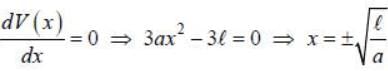
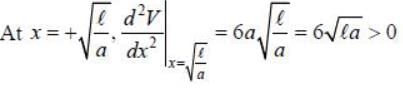
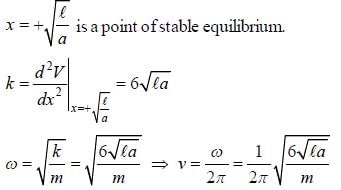
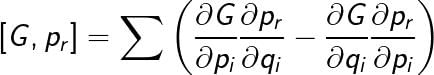
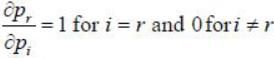
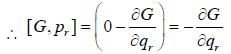

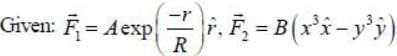
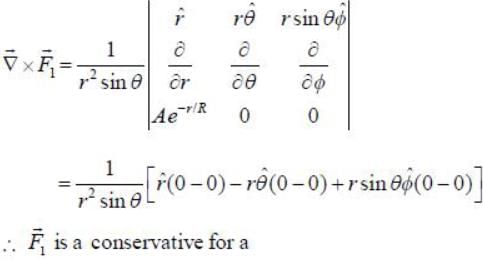

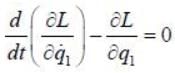
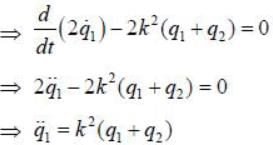
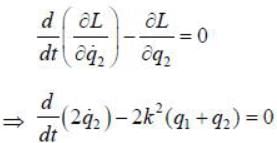
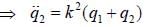
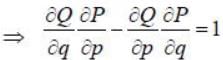
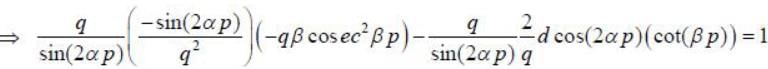

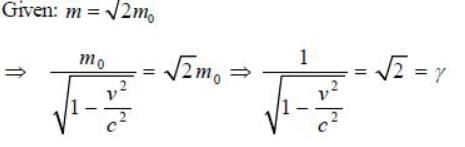



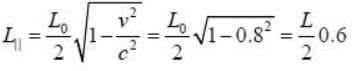
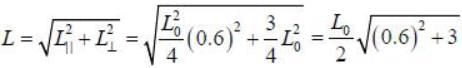
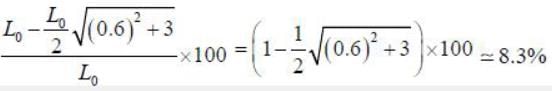
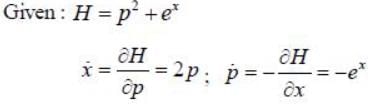
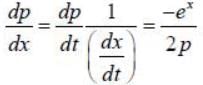
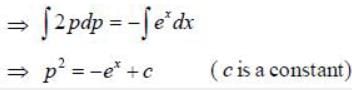
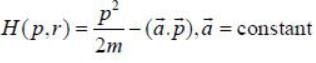
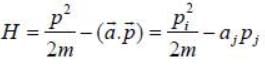
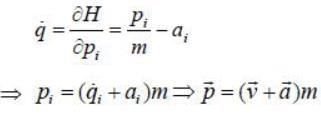
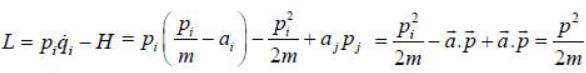
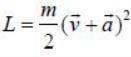
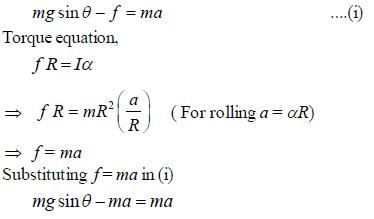
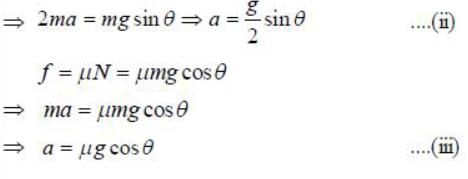
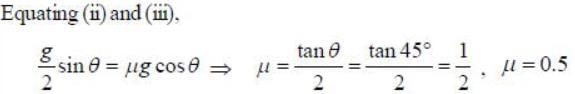
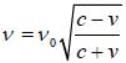
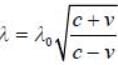
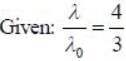
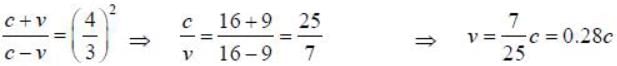

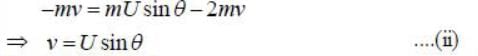

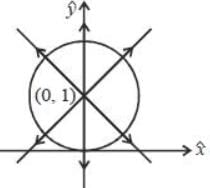
 is radially outwards). This means that V (r, θ, φ) decreases with radius. The gradient of a surface is in the direction along the maximum rate o f increase o f the function (here V (r, θ, φ)).
is radially outwards). This means that V (r, θ, φ) decreases with radius. The gradient of a surface is in the direction along the maximum rate o f increase o f the function (here V (r, θ, φ)). 
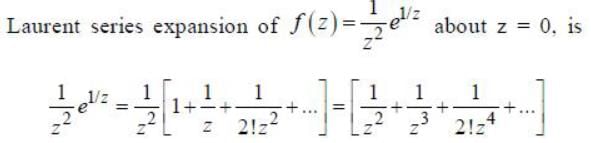
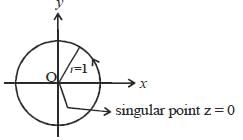
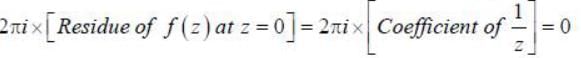
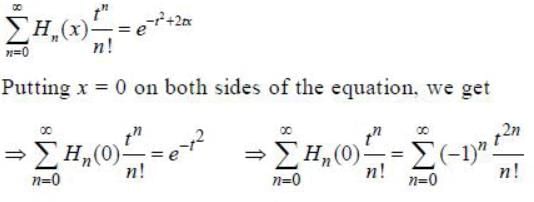
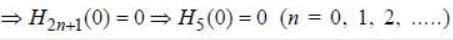
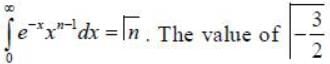 will be
will be 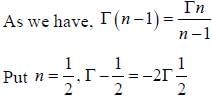
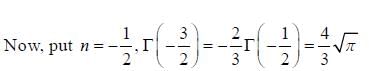
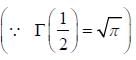
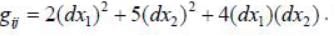 Then det (gij) = _____
Then det (gij) = _____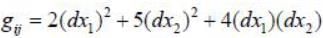
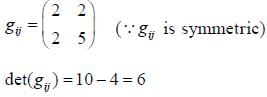
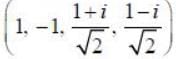 is the possible set of eigenvalues of a (4 x 4) unitary matrix
is the possible set of eigenvalues of a (4 x 4) unitary matrix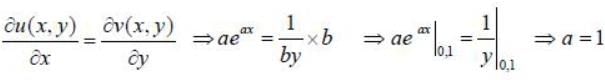
 has the dimension of [x]
has the dimension of [x]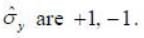
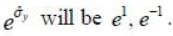
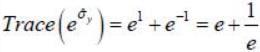
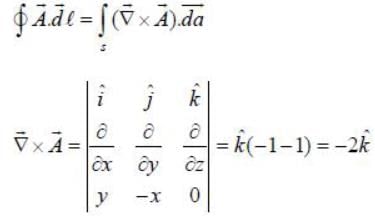
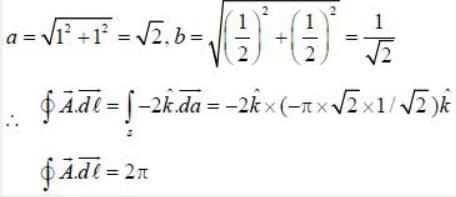
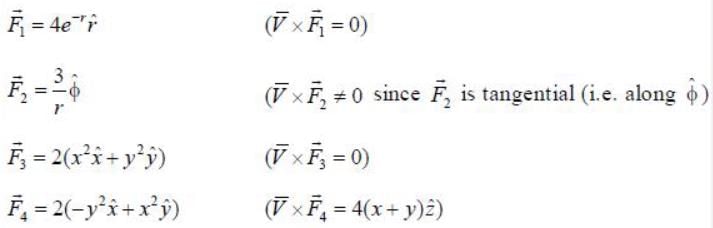
 only are conservative
only are conservative