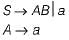Test: Pushdown Automata: CFL & DCFL- 2 - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test - Test: Pushdown Automata: CFL & DCFL- 2
For the grammar given below, what is the equivalent CFG without useless symbols
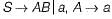
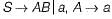
For the given grammar below, what is the equivalent CFG without ∈ -productions?
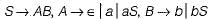
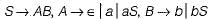
What is the equivalent CFL for the following CFG 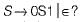
For the given grammar below, what is the equivalent CFG without ∈-productions?
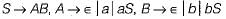
What is the equivalent CFL for the following CFG?
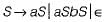
Which of the following statement is/are true?
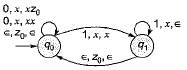
Which language does the following PDA accept 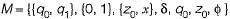 and b is given by
and b is given by
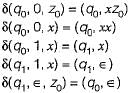
Which language does M accept if the following transition is added?
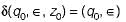
Consider the following set of languages:
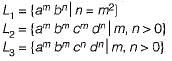
Which of the above language is not context free?
L1 has the following grammar:
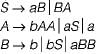
L2 has the following grammar:
S → Sba\a
Which of the following statement is true about?
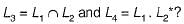
The reduced grammar equivalent to the grammar, whose production rules are given below, is
S → AB | CA
B → BC | AB
A → a
C → a B | b
Consider the CFG G( \/, T, P, S) with the following production:
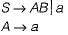
Let CFG G' is an equivalent CFG with no useless symbols. How many minimum production will be there in G'?


 both recursively enumerable, then both L and
both recursively enumerable, then both L and  are recursive.
are recursive.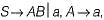 is useless and so is A. Hence
is useless and so is A. Hence 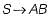 is useless. Therefore the equivalent CFG is S → a.
is useless. Therefore the equivalent CFG is S → a.
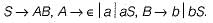

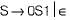
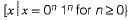
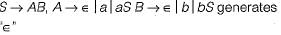
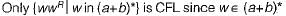 and we cannot determine the middle of the wwR i.e. we cannot determine the end of ' w" and start of wR. In all other options, there are more than one comparison.
and we cannot determine the middle of the wwR i.e. we cannot determine the end of ' w" and start of wR. In all other options, there are more than one comparison.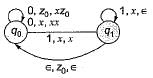
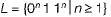
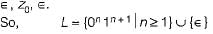
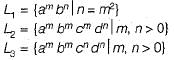
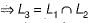 is a context free language,
is a context free language,