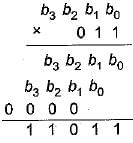Test: Basics of Digital Electronics- 2 - Electrical Engineering (EE) MCQ
20 Questions MCQ Test Topicwise Question Bank for Electrical Engineering - Test: Basics of Digital Electronics- 2
Which of the following statements about digital systems are correct?
1. These are easier to design compared to analog systems.
2. These are highly affected by unwanted electrical signals.
3. Accuracy and precision of digital systems are greater when compared with analog systems.
4. The fabrication of digital ICs is complicated and costly than that of analog ICs.
Choose the correct code from the given options:
1. These are easier to design compared to analog systems.
2. These are highly affected by unwanted electrical signals.
3. Accuracy and precision of digital systems are greater when compared with analog systems.
4. The fabrication of digital ICs is complicated and costly than that of analog ICs.
Choose the correct code from the given options:
Assertion (A): The advantage of performing subtraction by the complement method is reduction in the hardware.
Reason (R): Instead of having separate digital circuits for addition and subtraction, only adding circuits are needed for subtraction by complement method.
Reason (R): Instead of having separate digital circuits for addition and subtraction, only adding circuits are needed for subtraction by complement method.
The decimal equivalent of the hexadecimal number (A0F9.0EB)16 is
If 100b = 1610, then the value of b would be equal to
Consider the following series with a missing number;
10000,121,100, ?, 24, 22, 20
If in the above series, the same integer is expressed in different number systems, the missing number of the series would be equal to
Each of the following arithmetic operations is correct in at least one number system:
(i) 1234 + 5432 = 6666 is valid in any number system with base ≥ 6.
(ii) √41 = 5 is valid in a number system with base 6.
(iii) 302/20 = 12.1 is valid in a number system with base 5.
Out of the above arithmetic operations:
Consider the following statements:
1. In a self-complementing code, the code word for the 9's complement of N is the 1’s complement of the codeword for N.
2. Each one of the 4-bit BCD codes has 6 illegal states.
3. The Gray code cannot be used for mathematical operations.
4. Excess-3 code can be used for mathematical operations.
Which of the statements given above is/are correct?
Assertion (A): The 2’s complement system has two zeros, a positive 0 (all 0s) and a negative 0 (all 1’s).
Reason (R): The complement of the complement gives the original number
Assertion (A): The computer method of division requires successive subtraction.
Reason (R): The computer method of multiplication requires repeated addition.
Assertion (A): Gray code is sometimes called reflective code.
Reason (R): The n least significant bits for 2n through (2n +1- 1) are the mirror images for 0 through (2n-1).
Which of the following 4-bit binary pairs does not forms a Gray code pair?
Match List-I (Data representation) with List-ll (Range with n-bits) and select the correct answer using the codes given below the lists:
List-1
A. Signed numbers in 1 ’s complement form
B. Signed magnitude
C. Unsigned magnitude
D. Signed numbers in 2’s complement form
List-ll
1. 0 to (2n - 1)
2. -(2n -1) to + (2n -1 - 1)
3. -(2n -1) to (2n -1)
4. -(2n -1 - 1) to + (2n -1 - 1)
Codes:
A B C D
(a) 3 3 1 2
(b) 1 4 3 4
(c) 2 4 1 3
(d) 4 4 1 2
A number is represented in 2’s complement as (1101)2. It’s equivalent decimal number is
Match List-I with List-ll and select the correct answer using the codes given below the lists:
List-I
A. (345)8
B. (11011.011)2
C. (47)16
List-II
1. (1B.6)16
2. (229)10
3. (107)8
4. (326)10
5. (D8.7)16
Code:
A B C
(a) 2 5 3
(b) 4 3 2
(c) 2 1 3
(d) 4 1 2
Which of the following statements is/are correct in regard to excess-3 code?
Multiplication of two binary numbers A and B is 11011. If A = 011, then B is
Which of the following statement is not correct in regard to the “GRAY Code”?
Assertion (A): The “XS-3 code,” also called “Excess-3 code” is a non-weighted BCD code.
Reason (R): In XS-3 code, each binary code word is the corresponding 8421 code word plus 0011(3).





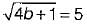

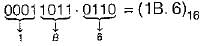 (Binary to Hexadecimal conversion)
(Binary to Hexadecimal conversion)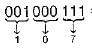 = (107)8
= (107)8