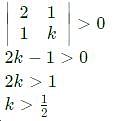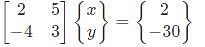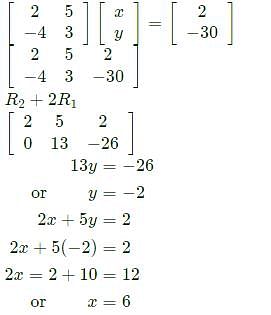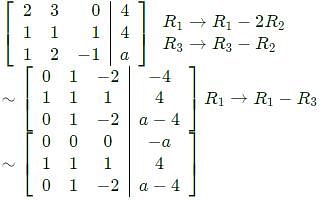Test: Differential Calculus - Civil Engineering (CE) MCQ
20 Questions MCQ Test Engineering Mathematics - Test: Differential Calculus
If an error of 1% is made in measuring the major and minor axes of an ellipse, then the percentage error in the area is approximately equal to
Consider the Assertion (A) and Reason (R) given below:
Reason (R): Given function u is homogeneous of degree 2 in x and y.
Of these statements
If u = x log xy, where x3 + y3 + 3xy = 1, then du/dx is equal to
The minimum distance from the point (4, 2) to the parabola y2 = 8x is
The co-ordinates of the point on the parabola y = x2 + 7x + 2 which is closest to the straight line y = 3x - 3, are
The shortest distance of the point (0, c), where 0 ≤ c ≤ 5, from the parabola y = x2 is
The minimum value of 3x+5y such that:
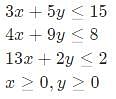
is ___________.
The condition for which the eigenvalues of the matrix
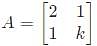
are positive, is
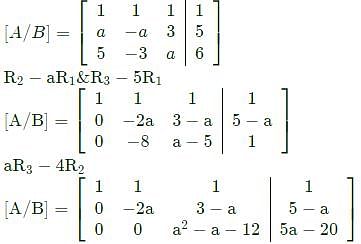
For what value of a, if any, will the following system of equations in x, y and z have a solution
2x + 3y = 4
x + y + z = 4
x + 2y - z = a
|
65 videos|122 docs|94 tests
|



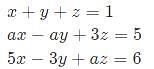
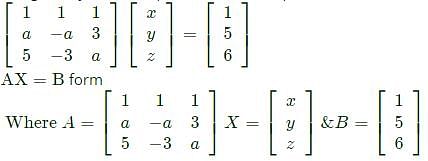
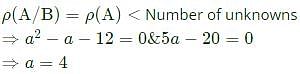

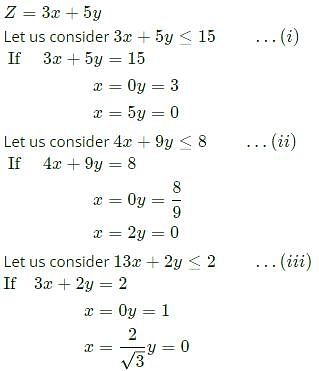
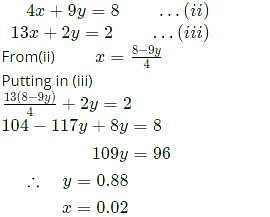
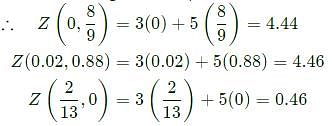
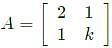 are positive
are positive