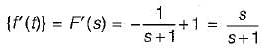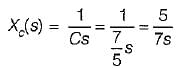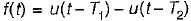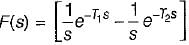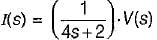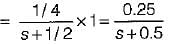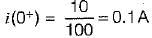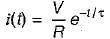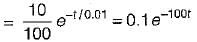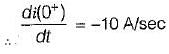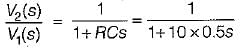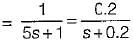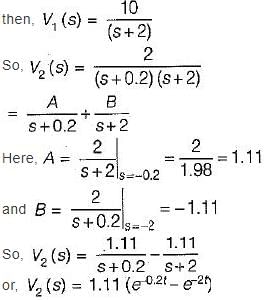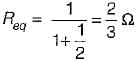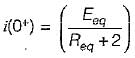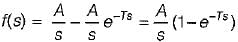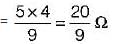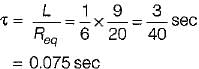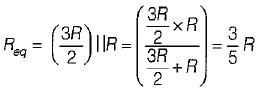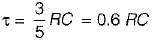Get the App Signup / Login
Sign in Open App

Test: First Order RL & RC Circuits- 2


15 Questions MCQ Test Topicwise Question Bank for Electrical Engineering | Test: First Order RL & RC Circuits- 2


Description
Attempt Test: First Order RL & RC Circuits- 2 | 15 questions in 45 minutes | Mock test for Electrical Engineering (EE) preparation | Free important questions MCQ to study Topicwise Question Bank for Electrical Engineering for Electrical Engineering (EE) Exam | Download free PDF with solutions
QUESTION: 1

Laplace transform analysis gives

Solution:
QUESTION: 2

The Laplace transform of the derivative of the signal f(t) = e-t u(t) is

Solution:

The derivative of function f(t) is
f'(t) = e-tδ (t) + u (t) (-e-t)
= -e-t u(t) + e-tδ(t)

QUESTION: 3

For a series R - C circuit excited by a dc voltage of 20 V, and with time-constant τ seconds, the voltage across the capacitor at time t = τ is given by

Solution:

Vc(t) = V(1 - e-t/τ) volts
V = 20 volt (given)
At t = τ, Vc|t = τ = 20 (1 - e-1) volts

QUESTION: 4

The Laplace-transform equivalent of a given network will have 7/5 F capacitor replaced by 5
Solution:

QUESTION: 5

An RC circuit has a capacitor C = 2 μF in series with a resistance R = 1 MΩ The time of 6 secs will be equal to
Solution:

Time constant of series RC circuit is
τ = RC = 1 x 106 x 2 x 10-6
= 2 secs
Hence, time of 6 seconds will be equal to 3τ = 3 times of time constant.

QUESTION: 6

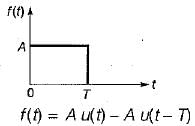
The Laplace transform of the gate function shown below is
Solution:

From the given waveform, we have

∴ 

QUESTION: 7

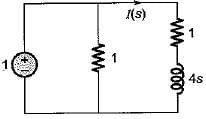
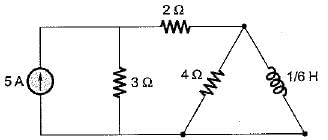
Assuming initial condition to be zero, the current i(t) in the circuit shown below is
Solution:

The given circuit in Laplace domain is shown below.

Here 

(Using current divider theorem)

or, i(t) = 0.25 e-0-5t u(t)

QUESTION: 8

A 10 volts step voltage is applied across a RC series circuit at t = 0 having R = 100 Ω, and C = 100 μF.
The values of i(t) and di(t)/dt at t = 0 are respectively given by
Solution:


At t = 0, capacitor acts as short-circuit.
So, 

Time constant of given circuit is
τ = RC = 100 x 100 x 10-6
= 10-2 sec = 0.01 sec
With zero initial condition, current in the series RC circuit is


Hence, 
di/dt = -10 e-100t
i(0+) = 0.1 A

QUESTION: 9

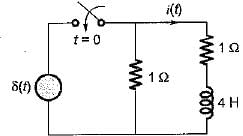
If the input voltage V1(t) = 10 e-2t V then, the output voltage V2(t) for the circuit shown below is
Solution:

Given circuit is a low-pass filter having transfer function


When, V1(t) = 10e-2t

QUESTION: 10

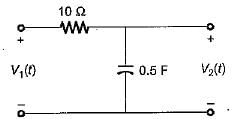
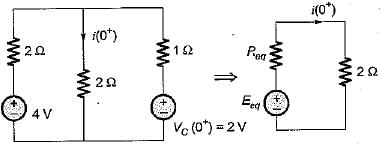
In the circuit shown below, the switch 'S' is opened at t = 0. Prior to that, switch was closed.

The current i(t) is at t = 0+ is
Solution:

For t = 0-, switch Sis closed. Hence, in steady state capacitor will act as open circuit.
Thus, V0(0-) = VC(0+) = 2 volts
The circuit at t = 0+ is shown below where,
cananitor ants as a constant voltage source.

Using source transformation,

and 

Hence, 

QUESTION: 11

A rectangular pulse of duration T and magnitude A has the Laplace transform
Solution:


∴ 

QUESTION: 12

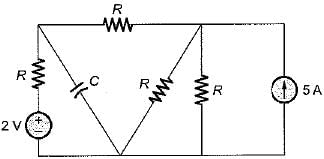
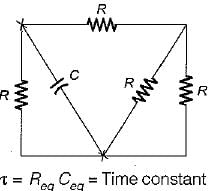
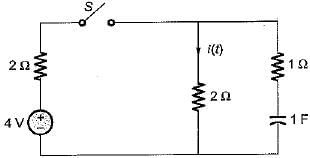
The time constant of the circuit shown below is
Solution:

Reg across inductor 

(5 A C.S open circuited)
∴ Time constant of RL circuit is

QUESTION: 13

Assertion (A): Laplace transform is preferred for solving networks involving higher order differential equations.
Reason (R): The classical method for solving differential equations of higher order is quite cumbersome.
Solution:
QUESTION: 14

Assertion (A): In a purely capacitive circuit, the current wave is more distorted than the voltage wave.
Reason (R): The harmonics in the current wave are increased in proportion to their frequency numbers.
Solution:
QUESTION: 15

The time constant of the circuit shown below is
Solution:

For finding time constant of the circuit 5 A current source is open circuited and 2 V voltage source is short circuited.


Ceq = C
∴ 

Use Code STAYHOME200 and get INR 200 additional OFF
Use Coupon Code
Use Coupon Code

Recommended Content

Recommended Tests

Download free EduRev App

Track your progress, build streaks, highlight & save important lessons and more!
© EduRev
Follow Us