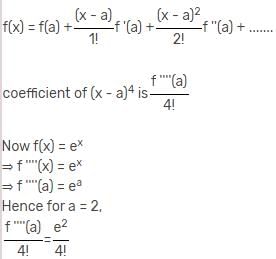Test: Fourier Series, Numerical Methods & Complex Variables- 1 - Engineering Mathematics MCQ
20 Questions MCQ Test Engineering Mathematics - Test: Fourier Series, Numerical Methods & Complex Variables- 1
The Fourier series of a real periodic function has only
P. cosine terms if it is even
Q. sine terms if it is even
R. cosine terms if it is odd
S. sine terms if it is odd
Which of the above statements are correct?
For the function e–x, the linear approximation around x = 2 is
In the Taylor series expansion of exp(x) + sin(x) about the point x = π, the coefficient of (x – π)2 is
The function x(t) is shown in the figure. Even and odd parts of a unit-step function u(t) are respectively,
In the Taylor series expansion of ex about x = 2, the coefficient of (x - 2)4 is
The Fourier series expansion of a symmetric and even function, f(x) where
Will be
The Fourier series expansion of the periodic signal shown below will contain the following nonzero terms
The Fourier series for the function f(x)=sin2x is
X(t) is a real valued function of a real variable with period T. Its trigonometric Fourier Series expansion contains no terms of frequency ω = 2π (2k ) /T ; k = 1, 2,.... Also, no sine terms are present. Then x(t) satisfies the equation
The residue of the function f(z)
The residues of a complex function at its poles are
The value of the contour integral in positive sense is
The integral evaluated around the unit circle on the complex plane for
An analytic function of a complex variable z = x + iy is expressed as f(z) = u (x, y) + i v(x, y) where i =√−1 . If u = xy, the expression for v should be
The analytic function has singularities at
The value of the integral (where C is a closed curve given by |z| = 1) is
Roots of the algebraic equation x3 +x2 +x+ 1 = 0 are
The algebraic equation
F (s ) = s5 − 3s4+ 5s3− 7s2 + 4s + 20 is given F ( s ) = 0 has
|
65 videos|133 docs|94 tests
|