Test: Fourier Series, Numerical Methods & Complex Variables- 2
30 Questions MCQ Test GATE Mechanical (ME) 2023 Mock Test Series | Test: Fourier Series, Numerical Methods & Complex Variables- 2
| 1 Crore+ students have signed up on EduRev. Have you? |
Choose the function f(t); –∞ < t < ∞, for which a Fourier series cannot be defined.
Fourier series is defined for periodic function and constant.
Fourier series can’t be defined for non-periodic functions.
The sum of two periodic function is also a periodic function.
3 sin (25 t) is a periodic function
4 cos (20 t + 3) and 2 sin (710 t) both are periodic function. So, 4 cos (20t + 3) + 2 sin (710 t) is also a periodic function.
e-|t| sin (25 t) is not a periodic function. So, Fourier series is can’t be defined.
1 is a constant. So, Fourier series is defined.
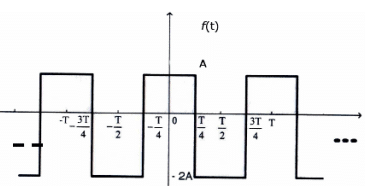
The trigonometric Fourier series for the waveform f(t) shown below contains
From figure it’s an even function. so only cosine terms are present in the series and for DC value,
So DC take negative value.
Which of the following functions would have only odd powers of x in its Taylor series expansion about the point x = 0?
The Taylor series expansion of 
We know.
The sum of the infinite series, 
The summation of series 
Fourier series for the waveform, f (t) shown in fig. is
From the figure, we say f (x) is even functions. so choice (c) is correct.
The Fourier Series coefficients, of a periodic signal x (t), expressed as
are given by 
For the function of a complex variable W = ln Z (where, W = u + jv and Z = x + jy), the u = constant lines get mapped in Z-plane as
Given,
ii, where i = √−1, is given by
Assuming 
and t is a real number 
The modulus of the complex number 
Using Cauchy’s integral theorem, the value of the integral (integration being taken in counter clockwise direction) 
Here f (z) has a singularities at z i / 3
Which one of the following is NOT true for complex number Z1and Z2 ?
(a) is true since
(b) is true by triangle inequality of complex number.
(c) is not true since |Z1 − Z2 |≥|Z1 |– |Z2 |
(d) is true since
For the equation, s3 - 4s2 + s + 6 =0
The number of roots in the left half of s-plane will be
Constructing Routh-array
Number of sign changes in the first column is two, therefore the number of roots in the left half splane is 2
The value of the integral of the complex function
Along the path |s| = 3 is
f (s) has singularities at s =−1, −2 which are inside the given circle
For the function 
of a complex variable z, the point z = 0 is
Therefore the function has z = 0 is a pole of order 2.
The polynomial p(x) = x5 + x + 2 has
As, P(x) of degree 5 .So other four roots are complex.
If z = x + jy, where x and y are real, the value of |ejz| is
The root mean squared value of x(t) = 3 + 2 sin (t) cos (2t) is
x(t) = 3 + 2 sin t cos 2t
x(t) = 3 + sin 3t – sin t
∴ Root mean square value 
We wish to solve x2 – 2 = 0 by Netwon Raphson technique. Let the initial guess b x0 = 1.0 Subsequent estimate of x(i.e.x1) will be:
The order of error is the Simpson’s rule for numerical integration with a step size h is
The table below gives values of a function F(x) obtained for values of x at intervals of 0.25.
The value of the integral of the function between the limits 0 to 1 using Simpson’s rule is
A differential equation 
has to be solved using trapezoidal rule of integration with a step size h=0.01s. Function u(t) indicates a unit step function. If x(0-)=0, then value of x at t=0.01s will be given by
Consider the series 
obtained from the Newton-Raphson method. The series converges to
The series converges when X n+1= Xn =α
Given a>0, we wish to calculate its reciprocal value 1/a by using Newton-Raphson method :
for f(x) = 0. For a=7 and starting wkith x0 = 0.2. the first 2 iterations will be
With a 1 unit change in b, what is the change in x in the solution of the system of equations x + y = 2, 1.01 x + 0.99 y = b?
Given x + y = 2 …………….. (i)
1.01 x + 0.99 y = b …………….. (ii)
Multiply 0.99 is equation (i), and subtract from equation (ii), we get
The accuracy of Simpson's rule quadrature for a step size h is
|
27 docs|243 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
27 docs|243 tests
|
Download free EduRev App
Related content with Test: Fourier Series, Numerical Methods & Complex Variables- 2
|
|
Related tests with Test: Fourier Series, Numerical Methods & Complex Variables- 2
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
