Test: Introduction to Systems - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Introduction to Systems
A function f(t) is an even function, if for all values of (t)
( T is the time-period of the function)
A control system transfer function is H(s) = 1/s3. Express its impulse response in terms of unit step signal
The unit impulse response of a linear time invariant system is the unit step function u(t) for t > 0, the response of the system to an excitation e-at u(t), a > 0 will be
A system with an input x(t) and output y(t) is described by the relation: y(t) = tx(t). This system is
If a function f(t) u(t) is shifted to the right side by t0, then the function can be expressed as
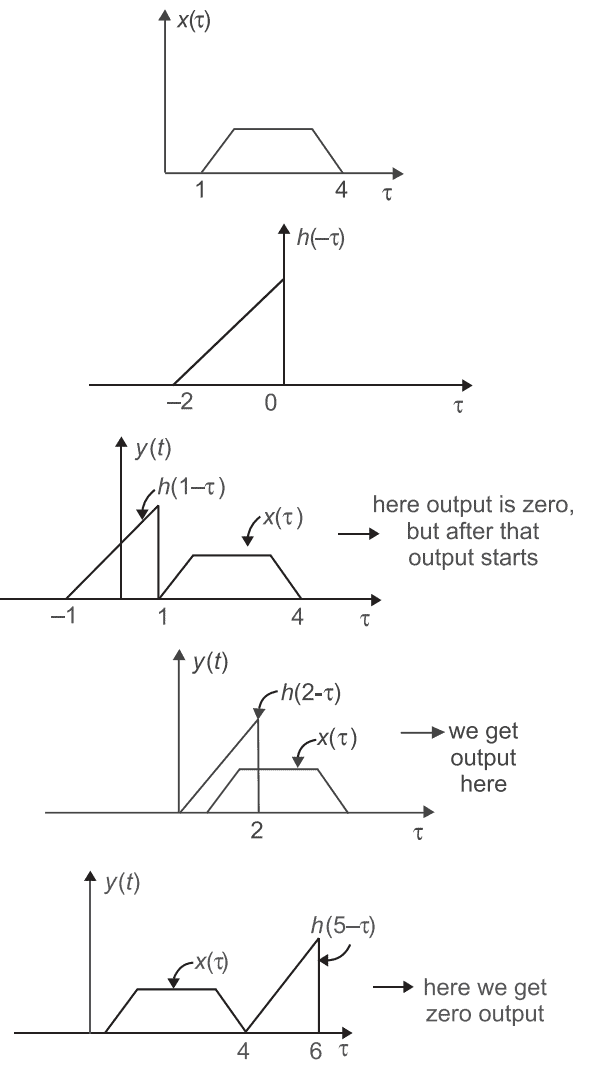
The impulse response of a causal, linear, time- invariant, continuous time system is h(t). The output y(t) of the same system to an input x(t). Where x(t) = 0 for t < -2 is
The unit step response of a system is given by (1 - e-αt) u(t), the impulse response is given by
Figure I and Figure II, shows the input x(t) to a linear time invariant system and the impulse response h(t) of the system

the output of the system is zero everywhere except for the time interval.
A signal f(t) = cos8πt + 0.5cos4πt is instantaneously sampled. The maximum allowable value of sampling interval Ts in sec is
The impulse response. h[n] of a linear time invariant system is given by h[n] = u[n + 3] + u[n - 3] - 2u[n - 7], the above system is




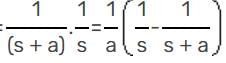

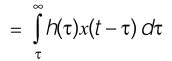
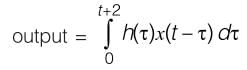
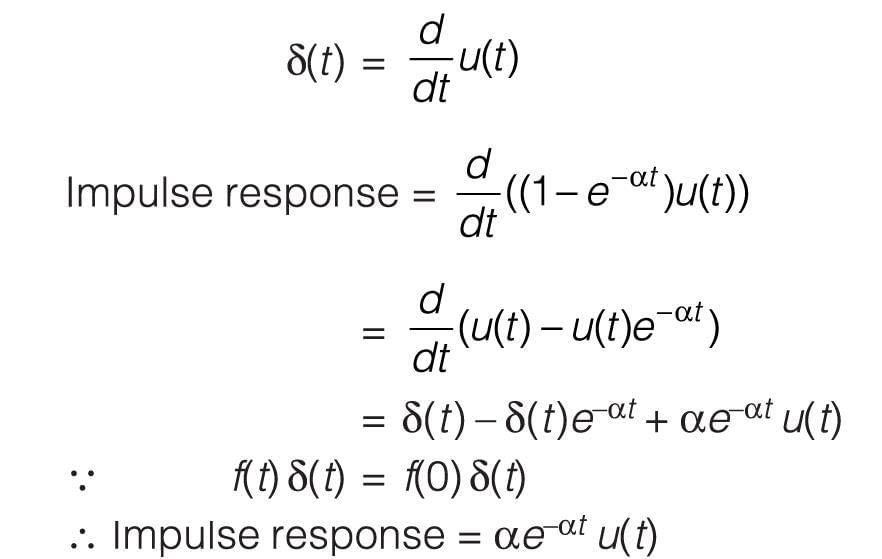
 ∞x(τ) h(t – τ)dτ– ∞
∞x(τ) h(t – τ)dτ– ∞