Test: Second Order RLC Circuits- 2 - Electrical Engineering (EE) MCQ
15 Questions MCQ Test - Test: Second Order RLC Circuits- 2
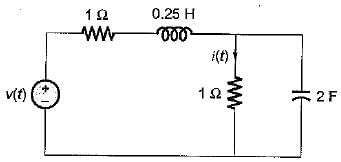
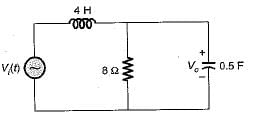
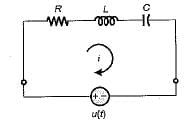
If the value of current i(t) for the circuit shown below is i(t) -20 e-2t, then the voltage source v(t) will be given by

The circuit shown in figure is critically damped.
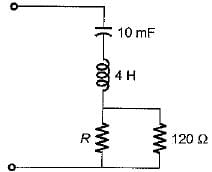
The value of R is

The value of R is
The voltage across a passive element in an electric circuit is given by 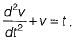 It is given that V(0+)
It is given that V(0+) 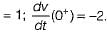
The value of v(t) is
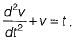 It is given that V(0+)
It is given that V(0+) 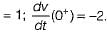
The value of v(t) is
A voltage is given by V(s) = 1/S(S + a). If V(∞) = 2 volts, then V(1) is
Transient current in an R-L-C circuit oscillatory when
Which of the following conditions are necessary for the validity of initial value theorem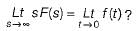
The poles and zeros of the transfer function 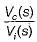 for the circuit shown below are located a
for the circuit shown below are located a
Assertion (A): Laplace transformation finds its application in solving the transient behaviour of the electric circuits.
Reason (R): The transient response of an electrical circuit can best be described by a linear differential equation.
The final value of f(t) = e-t (sin 2t + cos 5t) is
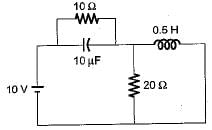
At t = 0+ with zero initial condition, the voltage across 20 Ω resistor is
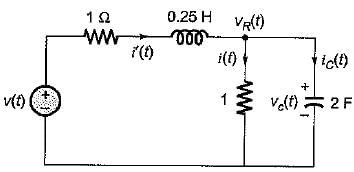
Assuming zero-initial condition vc(t) in the given circuit will be given by

The initial and final value of current through the resistor Rina series RLC circuit with unit step input and zero initial condition are respectively
Consider the following statements for a series RLC circuit excited with a voltage v(t)
1. For ξ, = 0, there is no-loss in the circuit.
2. The damping ratio of the circuit is independent of resistance R of the circuit.
3. The response of the circuit is oscillator if ξ value is more than unity.
Q. Which of the above statements is/are true?


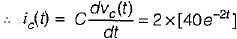
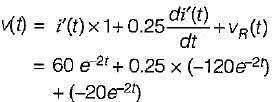
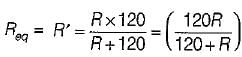
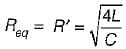
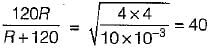

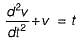
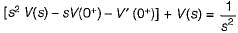
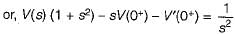

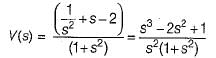
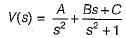
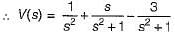
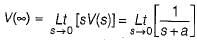
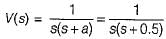

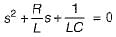
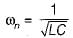
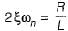
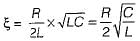
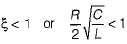
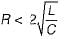
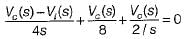
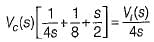
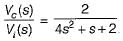
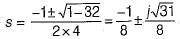
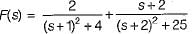
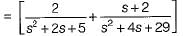
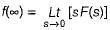
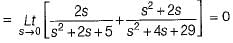

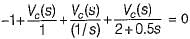

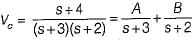
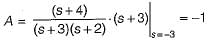
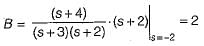
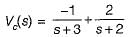
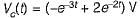
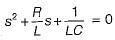 (characteristic equation)
(characteristic equation)











