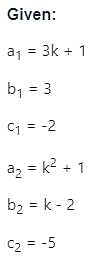Test: Systems of Linear Equations, Matrix Algebra & Transform Theory- 2
30 Questions MCQ Test GATE Mechanical (ME) 2023 Mock Test Series | Test: Systems of Linear Equations, Matrix Algebra & Transform Theory- 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider the system of equations given below:
x + y = 2
2x + 2y = 5
This system has
x + y = 2
2x + 2y = 5
This system has
(b) This can be written as AX = B Where A
Angemented matrix
rank(A) ≠ rank(
). The system is inconsistant .So system has no solution.
For what value of a, if any, will the following system of equations in x, y and z have a solution?
2x + 3y = 4
x+y+z = 4
x + 2y - z = a
2x + 3y = 4
x+y+z = 4
x + 2y - z = a
(b)
If a = 0 then rank (A) = rank(
) = 2. Therefore the system is consistant
∴ The system has soln .
Solution for the system defined by the set of equations
4y + 3z = 8;
2x – z = 2
and 3x + 2y =5 is
4y + 3z = 8;
2x – z = 2
and 3x + 2y =5 is
Ans.(d)
Consider the matrix A = 
,Now det (A) = 0
So byCramer's Rule the system has no solution
For what values of α and β the following simultaneous equations have an infinite numberof solutions?
x + y + z = 5; x + 3y + 3z = 9; x + 2y + αz = β
(d)
= 
For infinite solution of the system
α − 2 = 0 and β − 7 = 0
⇒ α = 2 and β = 7.
Let A be a 3 × 3 matrix with rank 2. Then AX = 0 has
(b)
We know , rank (A) + Solution space X(A) = no. of unknowns.
⇒2 + X(A) = 3 . [Solution space X(A)= No. of linearly independent vectors]
⇒ X(A) =1.
A is a 3 x 4 real matrix and A x = b is an inconsistent system of equations. The highest possible rank of A is
(b). Highest possible rank of A= 2 ,as Ax = b is an inconsistent system.
Consider the matrices X (4 × 3), Y (4 × 3) and P (2 × 3). The order or P (XTY)–1PT] T will be
(a)
Given matrix [A] = 
the rank of the matrix is
(c)
∴Rank(A) = 2
The Laplace transform of 
Ans. (b)False
Laplace transform of
There are two containers, with one containing 4 Red and 3 Green balls and the other containing 3 Blue and 4 Green balls. One bal is drawn at random form each container.The probability that one of the ball is Red and the other is Blue will be
If L defines the Laplace Transform of a function, L [sin (at)] will be equal to
Ans. (b)
⇒ 
The Inverse Laplace transform of 
is
Ans. (c)
Laplace transform for the function f(x) = cosh (ax) is
Ans. (b)
It is a standard result that
L (cosh at) = 
If F(s) is the Laplace transform of function f (t), then Laplace transform of 
Ans. (a)
Laplace transform of the function sin ωt
Ans. (b)
Laplace transform of (a + bt)2 where ‘a’ and ‘b’ are constants is given by:
Ans.(c) 
A delayed unit step function is defined as 
Its Laplace transform is
Ans. (d)
The Laplace transform of the function sin2 2t is
Ans.(a)
Find the rank of the matrix
To find out the rank of the matrix first find the |A|
If the value of the |A| = 0 then the matrix is said to be reduced
But, as the determinant of A has some finite value, then the rank of the matrix is 3.
The running integrator, given by 
Ans. (b)
The state transition matrix for the system X- = AX with initial state X(0) is
Ans. (c)
The Fourier transform of x(t) = e–at u(–t), where u(t) is the unit step function
Ans. (d)
The fundamental period of the discrete-time signal 
is
Ans. (b)
or 
or 
u(t) represents the unit step function. The Laplace transform of u(t – ζ) is
Ans. (c)
f(t) = u(t – ζ)
L{f(t)} = L{u(t – ζ)}
The fundamental period of x(t) = 2 sin πt + 3 sin 3πt, with t expressed in seconds, is
Ans. (d)
H.C.F. of 2π and 3π is 6π.
Then, fundamental frequency = 6π
∴ Period, T = 
= 3 sec
If the Fourier transform of x[n] is X(ejω), then the Fourier transform of (–1)n x[n] is
Ans. (c)
Given f(t) and g(t) as shown below:
g (t) can be expressed as
Given f(t) and g(t) as shown below:
The Laplace transform of g(t) is
Ans. (c)
The Laplace transform of g(t) is
Ans. (c)
Let Y(s) be the Laplace transformation of the function y (t), then final value of the function is
Ans. (c)
|
27 docs|243 tests
|
|
27 docs|243 tests
|
Download free EduRev App
(Scan QR code)
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
