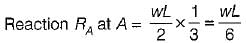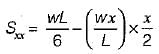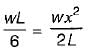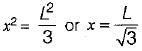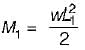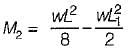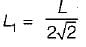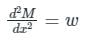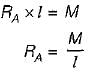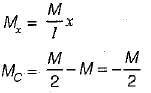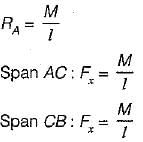Test: Shear Force & Bending Moment - 1 - Civil Engineering (CE) MCQ
10 Questions MCQ Test GATE Civil Engineering (CE) 2026 Mock Test Series - Test: Shear Force & Bending Moment - 1
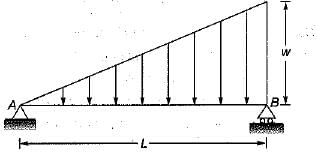
For the loaded beam shown in the figure, the correct shear force diagram is
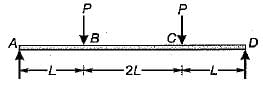

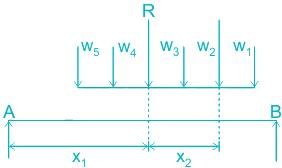
For the simply supported beam, shown in the figure below at what distance from the support A is the shear force zero?

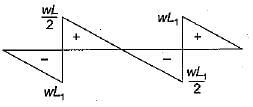
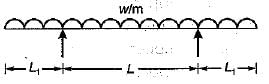
For the beam shown ih the given figure, the maximum positive bending moment is equal to the maximum negative bending moment. The value of L1 is

The maximum bending moment under a particular point load among a train of point loads crossing a simply Supported girder occurs at the location when that load is at
If a beam is subjected to a constant bending moment along its length then the shear force will
If the magnitude of shear force is constant, then the magnitude of the slope of bending moment curve is
Bending moment in the a beam is not a function of
If the bending moment diagram for a simply suppoted beam is of the form as given in figure then the load acting on the beam is
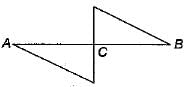
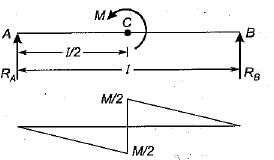
A beam is simply supported at its ends and is loaded by a couple at its mid-span as shown in figure. Shear force diagram for the beam is given by the figure
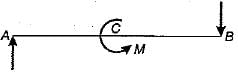
The point where the bending moment is zero after changing its sign is known as
|
31 docs|280 tests
|