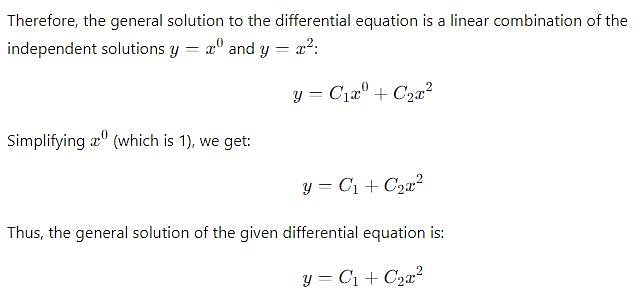Test: Differential Equations & Multiple Integrals- 1 - Mechanical Engineering MCQ
20 Questions MCQ Test GATE Mechanical (ME) Mock Test Series 2025 - Test: Differential Equations & Multiple Integrals- 1
A triangle ABC consists of vertex points A (0,0) B(1,0) and C(0,1). The value of the integral 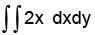 over the triangle is
over the triangle is
The area enclosed between the parabala y = x2 and the straight line y = x is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Changing the order of the integration in the double integral

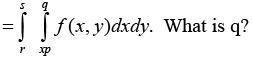
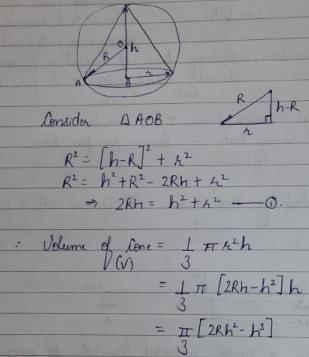
The right circular cone of largest volume that can be enclosed by a sphere of 1 m radius has a height of
the parabolic arc is revolved around the x-axis. The volume of
What is the area common to the circles r = a and r = 2a cos θ?
The expression for the volume of a cone is equal to
f ( x,y ) is a continuous defined over ( x,y ) ∈ [0,1]× [0,1] . Given two constrains, x > y 2 and y > x 2 , the volume under f ( x,y ) is
The following differential equation has
A solution of the following differential equation is given by
For the differential equation the boundary conditions are
(i) y = 0 for x = 0, and
(ii) y = 0 for x = a
The form of non-zero solutions of y (where m varies over all integers) are
Which of the following is a solution to the differential equation
For the differential equation the general solution is
The solution of the differential equation
The solution of with the condition y(1)
A technique by which problems in analysis, in particular differential equations, are transformed into algebraic problems is called
The general solution of (x2 D2 – xD), y= 0 is :
For the particular integrals is
It is given that y" + 2y' + y = 0, y(0) = 0, y(1)=0. What is y (0.5)?
The partial differential equation
|
29 docs|220 tests
|
|
29 docs|220 tests
|