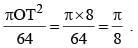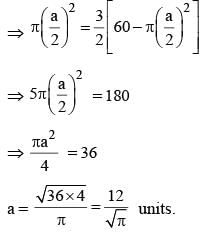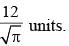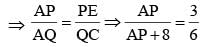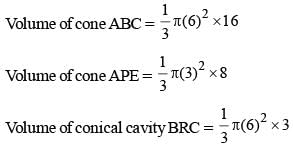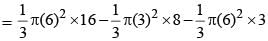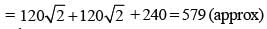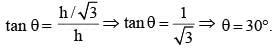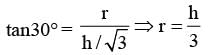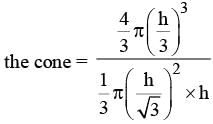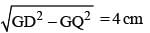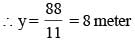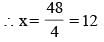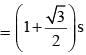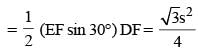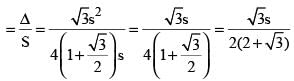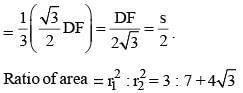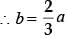Test: Mensuration - CAT MCQ
20 Questions MCQ Test Topic-wise Past Year Questions for CAT - Test: Mensuration
If the rectangular faces of a brick have their diagonals in the ratio 3 : 2√3 : √15 , then the ratio of the length of the shortest edge of the brick to that of its longest edge is
(2019)
Given an equilateral triangle T1 with side 24 cm, a second triangle T2 is formed by joining the midpoints of the sides of T1. Then a third triangle T3 is formed by joining the midpoints of the sides of T2. If this process of forming triangles is continued, the sum of the areas, in sq cm, of infinitely many such triangles T1, T2, T3,... will be
(2018)
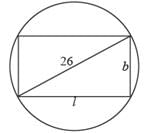
Let ABCD be a rectangle inscribed in a circle of radius 13 cm. Which one of the following pairs can represent, in cm, the possible length and breadth of ABCD?
(2018)
A right circular cone, of height 12 ft, stands on its base which has diameter 8 ft. The tip of the cone is cut off with a plane which is parallel to the base and 9 ft from the base. With π = 22/7, the volume, in cubic ft, of the remaining part of the cone is
(2018)
A solid metallic cube is melted to form five solid cubes whose volumes are in the ratio 1 : 1 : 8 : 27 : 27. The percentage by which the sum of the surface areas of these five cubes exceeds the surface area of the original cube is nearest to
(2017)
A regular polygon has an even number of sides. If the product of the length of its side and the distance between two opposite sides is 1/4 th of its area, find number of sides it has
(2016)
A field is in the form of a rectangle of dimension 24 m × 56 m. There is 2700 m of fencing that is available. The field has to be divided into many identical smaller square plots, having integral sides (in metres), each of which is to be fenced. Find the side of each of the square plots such that the fencing material that is left out is minimum.
(2015)
ABCD is an isosceles trapezium with BC = AD = 10 units, AB = 2 units and CD = 14 units. The mid-points of the sides of the trapezium are joined to form a quadrilateral PQRS. Find the ratio of the area of the circle inscribed in the quadrilateral PQRS to the area of trapezium ABCD.
(2015)
The smallest possible circle touching two opposite sides of a rectangle is cut-out from a rectangle of area 60 sq. units. If the area of this circle is 3/2 times the area left out in the rectangle, find the length of the smaller side of the rectangle.
(2015)
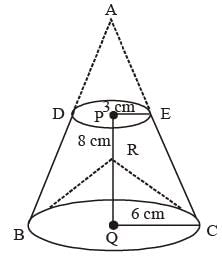
The top and bottom radii of a frustrum of a solid cone are 3 cm and 6 cm respectively. Its height is 8 cm. There is a conical cavity of height 3 cm and radius 6 cm at the bottom. The amount of material in the solid is
(2014)
The length of the hypotenuse of a right-angled triangle is 240 units. The perimeter of the given triangle is a perfect square. If the perimeter of the given triangle is greater than 550 units, then which of the following can be the length of a side of the given right-angled triangle?
(2014)
How many rectangles with integral sides are possible where the area of the rectangle equals the perimeter of the rectangle?
(2014)
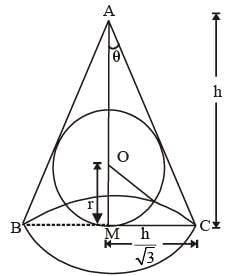
A spherical ball of the maximum possible volume is placed inside a right-circular cone of height ‘h’ units. If the radius of the base of the cone is equal to h/ √3 units, then the ratio of the volume of the sphere to that of the cone is
(2013)
How many triangles can be drawn by joining any three vertices of a pentagon?
(2013)
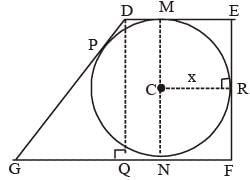
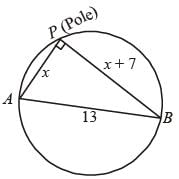
A trapezium DEFG is circumscribed about a circle that has centre at C. If DM = 1 cm, GN = 4 cm and the measure of ∠DEF = ∠EFG = 90°, then find the radius of the circle.
(2012)
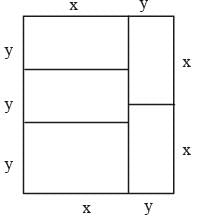
A rectangle with perimeter 88 m is partitioned into 5 congruent rectangles, as shown in the diagram given below. The perimeter of each of the congruent rectangles is
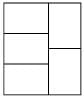
(2012)
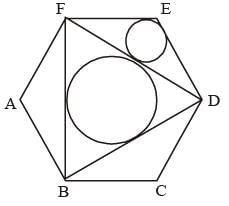
In the regular hexagon shown below, what is the ratio of the area of the smaller circle to that of the bigger circle?
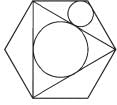
(2012)
A circle of radius 6.5 cm is circumscribed around a right-angled triangle with the sides a, b and c cm where a, b and c are natural numbers. What is the perimeter of the triangle?
(2012)
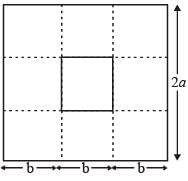
From a square piece of card-board measuring 2a on each side of a box with no top is to be formed by cutting out from each corner a square with sides b and bending up the flaps. The value of b for which the box has the greatest volume is
(2011)
A pole has to be erected on the boundary of a circular park of diameter 13 metres in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. The distance of the pole from one of the gates is:
(2011)
|
43 docs|31 tests
|


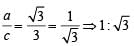



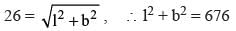
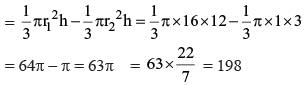
 ...(i)
...(i)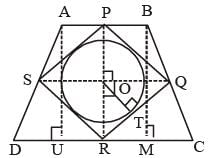
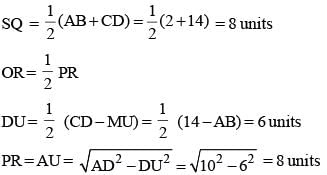
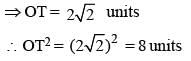
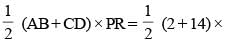 8 = 64 sq. unit.
8 = 64 sq. unit.