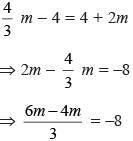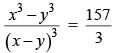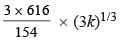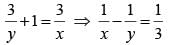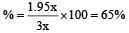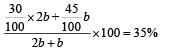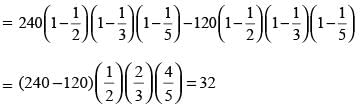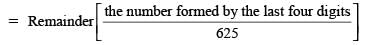Test: Number System - 1 - CAT MCQ
30 Questions MCQ Test 3 Months Preparation for CAT - Test: Number System - 1
How many factors of 24 × 35 × 104 are perfect squares which are greater than 1?
[2019]
How many pairs (m, n) of positive integers satisfy the equation m2 +105 = n2?
[2019]
In a six-digit number, the sixth, that is, the rightmost, digit is the sum of the first three digits, the fifth digit is the sum of first two digits, the third digit is equal to the first digit, the second digit is twice the first digit and the fourth digit is the sum of fifth and sixth digits. Then, the largest possible value of the fourth digit is
[2019]
The number of common terms in the two sequences: 15, 19, 23, 27, . . ., 415 and 14, 19, 24, 29, . . ., 464 is
[2019]
In an examination, the score of A was 10% less than that of B, the score of B was 25% more than that of C, and the score of C was 20% less than that of D. If A scored 72, then the score of D was
[2019]
If m and n are integers such that (√2)19 34 42 9m 8n = 3n 16m (∜64) then m is
[2019]
The product of two positive numbers is 616. If the ratio of the difference of their cubes to the cube of their difference is 157 : 3, then the sum of the two numbers is
[2019]
If (5.55)x = (0.555)y = 1000, then the value of 1/x - 1/y is
[2019]
The number of integers x such that 0.25 < 2x < 200, and 2x + 2 is perfectly divisible by either 3 or 4, is
[2018]
While multiplying three real numbers, Ashok took one of the numbers as 73 instead of 37. As a result, the product went up by 720. Then the minimum possible value of the sum of squares of the other two numbers is
[2018]
The number of girls appearing for an admission test is twice the number of boys. If 30% of the girls and 45% of the boys get admission, the percentage of candidates who do not get admission is
[2017]
A natural number n is such that 120 ≤ n ≤ 240. If HCF of n and 240 is 1, how many values of n are possible?
(2016)
If N = 888…up to 100 digits, what is the remainder when N is divided by 625?
(2016)
A sequence of 4 digits, when considered as a number in base 10 is four times the number it represents in base 6. What is the sum of the digits of the sequence?
(2016)
What is the remainder when 7700 is divided by 100?
(2016)
How many ordered triplets (a, b, c) exist such that LCM (a, b) = 1000, LCM (b, c) = 2000, LCM (c, a) = 2000 and HCF (a, b) = k × 125?
(2015)
Which of the following will completely divide (10690 – 4990)?
(2015)
Let P be the set of all odd positive integers such that every element in P satisfies the following conditions.
I. 100 ≤ n < 1000
II. The digit at the hundred’s place is never greater than the digit at tens place and also never less than the digit at units place.
How many elements are there in P?
(2015)
A four-digit number is divisible by the sum of its digits. Also, the sum of these four digits equals the product of the digits. What could be the product of the digits of such a number?
(2015)
P is the product of the first 100 multiples of 15 and Q is the product of the first 50 multiples of 2520. Find the number of consecutive zeroes at the end of P2/Q × 101767
(2015)
x is the smallest positive integer such that when it is divided by 7, 8 and 9 leaves remainder as 4, 5 and 6 respectively. Find the remainder when x3 + 2x2 – x – 3 is divided by 132.
(2015)
‘P’ is the product of ten consecutive two-digit natural numbers. If 2a is one of the factors of P, then the maximum value that ‘a’ can assume is
(2014)
If 7a = 26 and 343b = 676 then what is the relation between a and b?
(2014)
A set ‘P’ is formed from the set of first ‘N’ natural numbers by deleting all the perfect squares and all the perfect cubes. If the numbers are arranged in an ascending order then, what is the 476th number of the set ‘P’?
(2014)
Find the number of ways in which a batsman can score 100 runs by scoring runs in 2’s, 4’s and 6’s, such that he hits at least one double, one boundary and one six.
(2014)
The sequence P1, P2, P3, ..... is defined by P1 = 211, P2 = 375, P3 = 420, P4 = 523, and Pn = Pn-1 – Pn- 2 + Pn - 3 – Pn - 4 for all n3 5. What will be the value of P531 + P753 + P975?
(2014)
The ratio of two numbers whose sum is 600 is 7 : 8. What is the LCM of the given two numbers?
(2014)
The number of APs with 5 distinct terms that can be formed from the first 50 natural numbers is
(2014)
If f(n) = 14 + 24 + 34 + ... + n4, then how can 14 + 34 + 54 + ... + (2n – 1)4 be expressed?
(2014)
How many natural numbers divide exactly one out of 1080 and 1800, but not both?
(2013)
|
320 videos|428 docs|280 tests
|


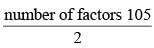

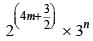
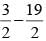 - 4
- 4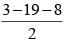

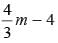 ...(i)
...(i)