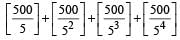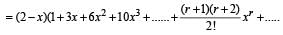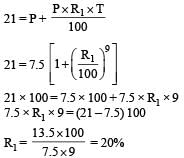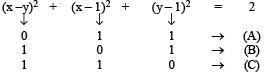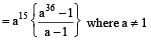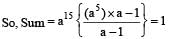Test: Number System - 2 - CAT MCQ
20 Questions MCQ Test 3 Months Preparation for CAT - Test: Number System - 2
The number of factors of the square of a natural number is 105. The number of factors of the cube of the same number is ‘F’. Find the maximum possible value of ‘F’.
(2013)
‘ab’ is a two-digit prime number such that one of its digits is 3. If the absolute difference between the digits of the number is nota factor of 2, then how many values can ‘ab’ assume?
(2013)
If E = 3 + 8 + 15 + 24 + … + 195, then what is the sum of the prime factors of E?
(2013)
Arrange the numbers 27/6, 33/4 and 52/3 in ascending order.
(2013)
The number 44 is written as a product of 5 distinct integers. If ‘n’ is the sum of these five integers then what is the sum of all the possible values of n?
(2012)
500! + 505! + 510! + 515! is completely divisible by 5n, where n is a natural number. How many distinct values of n are possible?
(2012)
A sequence of terms is defined such that 2an = an+1 + an-1 ; a0 = 1; a1 = 3 What is the value of a0 + a1 + a2 + 3 +......+ a50?
(2012)
There are five consecutive integers a, b, c, d and e such that a < b < c < d < e and a2 + b2 + c2 = d2 + e2. What is/are the possible value(s) of b?
(2012)
All the two-digit natural numbers whose unit digit is greater than their ten’s digit are selected. If all these numbers are written one after the other in a series, how many digits are there in the resulting number?
(2012)
(x – 1)(x – 2)(x – 3) = 6y. How many integer solutions exist for the given equation?
(2011)
A positive integer is equal to the square of the number of factors it has. How many such integers are there?
(2011)
(X + 3)/3, (X + 8)/4, (X + 15)/5, (X + 24)/6 ... ((X + 80)/10 is a sequence where X ≠ 1
What is the least value of X for which HCF (Numerator, Denominator) = 1 for each term of the given sequence?
(2011)
Let S denote the infinite sum 2 + 5x + 9x2 +14x3 + 20x4 + ....... , where | x | < 1 and the coefficient of xn-1 is 1/2 n(n + 3), (n = 1,2,.....) Then S equals
(2010)
Mr. Mehra is planning for higher education expenses of his two sons aged 15 and 12. He plans to divide ₹ 15 lakhs in two equal parts and invest in two different plans such that his sons may have access to ₹ 21 lakhs each when they reach the age of 21. He is looking for plan that will give him a simple interest per annum. The rates of interest of the plans for his younger son and elder son should be
(2010)
What is the number of non-negative integer solutions for the equation x2 – xy + y2 = x + y?
(2010)
If ‘a’ is one of the roots of x5 – 1 = 0 and a ≠ 1, then what is the value of a15 + a16 + a17 +.......a50?
(2010)
If x and y are positive integers, then the last digit of which of the following is same as the last digit of the sum of x and y?
(2010)
If ‘n’ is a natural number then the greatest integer less than or equal to (5 + √19)n
(2010)
P, Q and R are three consecutive odd numbers in ascending order. If the value of three times P is three less than two times R, find the value of R.
(2009)
|
320 videos|428 docs|280 tests
|