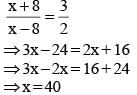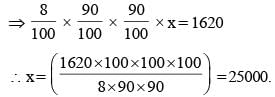Test: Percentage, Profit And Loss - CAT MCQ
30 Questions MCQ Test Topic-wise Past Year Questions for CAT - Test: Percentage, Profit And Loss
A person invested a total amount of ₹ 15 lakh. A part of it was invested in a fixed deposit earning 6% annual interest, and the remaining amount was invested in two other deposits in the ratio 2 : 1, earning annual interest at the rates of 4% and 3%, respectively. If the total annual interest income is ₹ 76000 then the amount (in ₹ lakh) invested in the fixed deposit was
(2019)
In a class, 60% of the students are girls and the rest are boys. There are 30 more girls than boys. If 68% of the students, including 30 boys, pass an examination, the percentage of the girls who do not pass is
(2019)
The income of Amala is 20% more than that of Bimala and 20% less than that of Kamala. If Kamala’s income goes down by 4% and Bimala’s goes up by 10%, then the percentage by which Kamala’s income would exceed Bimala’s is nearest to
(2019)
On selling a pen at 5% loss and a book at 15% gain, Karim gains ₹ 7. If he sells the pen at 5% gain and the book at 10% gain, he gains ₹ 13. What is the cost price of the book in Rupees?
(2019)
In 2010, a library contained a total of 11500 books in two categories - fiction and nonfiction. In 2015, the library contained a total of 12760 books in these two categories. During this period, there was 10% increase in the fiction category while there was 12% increase in the non-fiction category. How many fiction books were in the library in 2015?
(2019)
Amal invests ₹ 12000 at 8% interest, compounded annually, and ₹10000 at 6% interest, compounded semi-annually, both investments being for one year. Bimal invests his money at 7.5% simple interest for one year. If Amal and Bimal get the same amount of interest, then the amount, in Rupees, invested by Bimal is
(2019)
Mukesh purchased 10 bicycles in 2017, all at the same price. He sold six of these at a profit of 25% and the remaining four at a loss of 25%. If he made a total profit of ₹ 2000, then his purchase price of a bicycle, in Rupees, was
(2019)
A shopkeeper sells two tables, each procured at cost price p, to Amal and Asim at a profit of 20% and at a loss of 20%, respectively. Amal sells his table to Bimal at a profit of 30%, while Asim sells his table to Barun at a loss of 30%. If the amounts paid by Bimal and Barun are x and y, respectively, then (x – y)/p equals
(2019)
A trader sells 10 litres of a mixture of paints A and B, where the amount of B in the mixture does not exceed that of A. The cost of paint A per litre is Rs. 8 more than that of paint B. If the trader sells the entire mixture for Rs. 264 and makes a profit of 10%, then the highest possible cost of paint B, in Rs. per litre, is
(2018)
In an examination, the maximum possible score is N while the pass mark is 45% of N. A candidate obtains 36 marks, but falls short of the pass mark by 68%. Which one of the following is then correct?
(2018)
John borrowed Rs.2,10,000 from a bank at an interest rate of 10% per annum, compounded annually. The loan was repaid in two equal installments, the first after one year and the second after another year. The first installment was interest of one year plus part of the principal amount, while the second was the rest of the principal amount plus due interest thereon. Then each installment, in Rs., is
(2018)
A wholesaler bought walnuts and peanuts, the price of walnut per kg being thrice that of peanut per kg. He then sold 8 kg of peanuts at a profit of 10% and 16 kg of walnuts at a profit of 20% to a shopkeeper. However, the shopkeeper lost 5 kg of walnuts and 3 kg of peanuts in transit. He then mixed the remaining nuts and sold the mixture at Rs. 166 per kg, thus making an overall profit of 25%. At what price, in Rs. per kg, did the wholesaler buy the walnuts?
(2018)
If a and b are integers of opposite signs such that (a + 3)2 : b2 = 9 : 1 and (a – 1)2 : (b – 1)2 = 4 : 1, then the ratio a2 : b2 is
(2017)
If Fatima sells 60 identical toys at a 40% discount on the printed price, then she makes 20% profit. Ten of these toys are destroyed in fire. While selling the rest, how much discount should be given on the printed price so that she can make the same amount of profit?
(2017)
In a market, the price of medium quality mangoes is half that of good mangoes. A shopkeeper buys 80 kg good mangoes and 40kg medium quality mangoes from the market and then sells all these at a common price which is 10% less than the price at which he bougth the good ones. His overall profit is
(2017)
If a seller gives a discount of 15% on retail price, She still makes a profit of 2%. Which of the following ensures that she makes a profit of 20%?
(2017)
Some friends planned to contribute equally to jointly buy a CD player. However, two of them decided to withdraw at the last minute. As a result, each of the others had to shell out one rupee more than what they had planned for. If the price (in ₹) of the CD player is an integer between 1000 and 1100, find the number of friends who actually contributed?
(2016)
Balram, the local shoe shop owner, sells four types of footwear – Slippers (S), Canvas Shoes (C), Leather Shoes (L) and Joggers(J). The following information is known regarding the cost prices and selling prices of these four types of footwear:
(i) L sells for ₹ 500 less than J, which costs ₹ 300 more than S, Which, in turn, sells for ₹200 more than L.
(ii) L costs ₹ 300 less than C, which sells for ₹ 100 more than S, which, in turn, costs ₹ less than C.
If it is known that Balram never sells any item at a loss, then which of the following is true regarding the profit percentages earned by Balram on the items L, S, C and J represented by l, s, c and j
(2016)
The total cost of 2 pencils, 5 erasers, and 7 sharpeners is ₹ 30, while 3 pencils and 5 sharpeners cost ₹ 15 more than 6 erasers. By what amount (in ₹) does the cost of 39 erasers and 1 sharpener exceed the cost of 6 pencils?
(2016)
A shopkeeper sold 10 items, all of which are of the same cost price, such that profit percentage on no two item is the same. The profits made on the given items were in an arithmetic progression. If the profit percentage of the item the selling price of which is 4th highest and the item the selling price of which is 7th highest were 13 % and 10 % respectively, find the profit percentage on the whole.
(2015)
There are two factories – A and B – in Kaarobaarnagar. In factory A, the number of male employees is 50% more than that of female employees. In factory B, the number of female employees is 40% less than that of male employees. The number of female employees in factory B is 60 more than that of male employees in factory A. Which of the following cannot be the total number of male employees in the two factories put together?
(2014)
The percentage volumes of milk in three solutions A, B and C from a geometric progression in the order. If we mix the first, second and third solutions in the ratio 2 : 3 : 4 by volume, we obtain a solution containing 32% milk. If we mix them in the ratio 3 : 2 : 1, by volume, we obtain a solution containing 22% milk, What is the percentage of milk in A?
(2014)
An empty metal container (without its handle) weighs 15% of what it weighs when completely filled with a particular liquid. After adding the handle, the weight of the fully filled container increases by 5%. If the weight of a partly filled container is 1/3 of the completely filled container with the handle attached, then what fraction of container is utilized?
(2014)
A trader used to make 5% profit on an item by selling it at the usual marked price. One day, he tripled the marked price of the item and finally offered a discount of 30%. Find the percentage profit he made on the item that day.
(2014)
A shopkeeper sells four qualities of rice A, B, C and D having cost price ₹ 40/kg, ₹ 55/kg, ₹ 50/kg and ₹ 65/kg respectively. Ankit purchased ‘a’ kg of A and ‘b’ kg of B to make ‘a + b’ kg of a new quality ‘E’ of rice worth ₹ 50/kg. Then he purchased ‘c’ kg of C and ‘d’ kg of D to make ‘c + d’ kg of a new quality ‘F’ of rice worth ₹ 60/kg.
Finally he took ‘x’ kg of rice and ‘y’ kg of rice from ‘E’ quality of rice and ‘F’ quality of rice respectively to make ‘x + y’ kg of rice worth ₹ 53/kg. Ensuring that a, b, c, d, x and y are all integers then what is the minimum value of a + b + c + d + x + y in kg?
(2014)
The list price of an article was increased by 10%. It was then decreased by 10%. If the final price became ₹. 20, then find the initial
list price (in ₹.)
(2012)
A contractor did not have space in his garage for 8 of his trucks. He, therefore, increased the size of his garage by 50% which gave him space for 8 more trucks than he owned altogether. How many trucks did he own?
(2012)
10% of the voters did not cast their vote in an election between two candidates. 10% of the votes polled were found invalid. The successful candidate got 54% of the valid votes and won by a majority of 1620 votes. The number of voters enrolled on the voters list was :
(2011)
Ramit sold a table at a profit of 15%. Had he bought it at 10% less and sold it for ₹ 21 less, he would have gained 25%. At what price (in ₹) had he bought the table?
(2010)
In an examination, the average marks obtained by students who passed was x %, while the average of those who failed was y %. The average marks of all students taking the exam was z %. Find in terms of x, y and z, the percentage of students taking the exam who failed.
(2009)
|
43 docs|31 tests
|



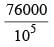

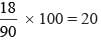













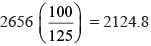
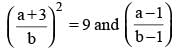




 for making 20% profit
for making 20% profit


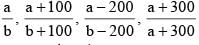

 and k is a +ve quantity, the above ratios can be rearranged as
and k is a +ve quantity, the above ratios can be rearranged as

 ...(i)
...(i)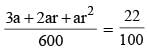 ...(ii)
...(ii)






 x initial list price = final list price
x initial list price = final list price