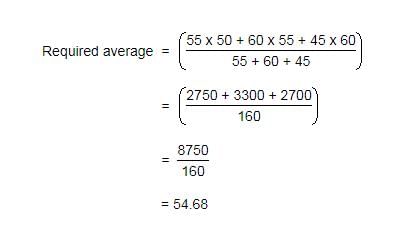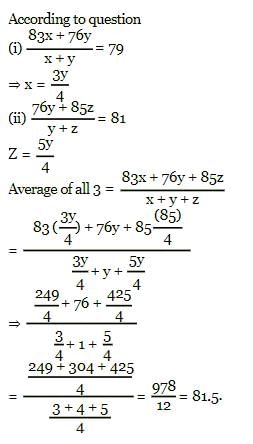Practice Test: Averages - 2 - Telangana Police Constable MCQ
10 Questions MCQ Test - Practice Test: Averages - 2
A grocer has a sale of Rs. 6435, Rs. 6927, Rs. 6855, Rs. 7230 and Rs. 6562 for 5 consecutive months. How much sale must he have in the sixth month so that he gets an average sale of Rs. 6500?
The average weight of A, B and C is 45 kg. If the average weight of A and B be 40 kg and that of B and C be 43 kg, what is the weight of B?
If the average marks of three batches of 55, 60 and 45 students respectively is 50, 55, 60, what is the average marks of all the students?
The average age of husband, wife and their child 3 years ago was 27 years and that of wife and the child 5 years ago was 20 years. What is the present age of the husband?
The average weight of 8 person's increases by 2.5 kg when a new person comes in place of one of them weighing 65 kg. What is the weight of the new person?
There are two divisions A and B of a class, consisting of 36 and 44 students respectively. If the average weight of divisions A is 40 kg and that of division b is 35 kg. What is the average weight of the whole class?
A batsman makes a score of 87 runs in the 17th inning and thus increases his averages by 3. What is his average after 17th inning?
A student needed to find the arithmetic mean of the numbers 3, 11, 7, 9, 15, 13, 8, 19, 17, 21, 14 and x. He found the mean to be 12. What is the value of x?
Arun obtained 76, 65, 82, 67 and 85 marks (out in 100) in English, Mathematics, Chemistry, Biology and Physics. What is his average mark?
Three classes X, Y and Z take an algebra test.
The average score in class X is 83.
The average score in class Y is 76.
The average score in class Z is 85.
The average score of all students in classes X and Y together is 79.
The average score of all students in classes Y and Z together is 81.
What is the average for all the three classes?


 Required sale = Rs. [ (6500 x 6) - 34009 ]
Required sale = Rs. [ (6500 x 6) - 34009 ] B's weight = 31 kg.
B's weight = 31 kg.