Test: Speed, Time & Distance - 1 - Bank Exams MCQ
20 Questions MCQ Test - Test: Speed, Time & Distance - 1
A person crosses a 600 m long street in 5 minutes. What is his speed in km per hour?
Q. A man takes 5 hours 45 min in walking to a certain place and riding back. He would have gained 2 hours by riding both ways. The time he would take to walk both ways, is:
Excluding stoppages, the speed of a bus is 54 kmph and including stoppages, it is 45 kmph. For how many minutes does the bus stop per hour?
A man complete a journey in 10 hours. He travels first half of the journey at the rate of 21 km/hr and second half at the rate of 24 km/hr. Find the total journey in km.
A car traveling with 5/7 of its actual speed covers 42 km in 1 hr 40 min 48 sec. What is the actual speed of the car?
A friend is spotted by Lalloo at a distance of 200 m. When Lalloo starts to approach him, the friend also starts moving in the same direction as Lalloo. If the speed of his friend is 15 kmph, and that of Lalloo is 20 kmph, then how far will the friend have to walk before Lalloo meets him?
A and B walk around a circular track. A and B walk at a speed of 2 rounds per hour and 3 rounds per hour respectively. If they start at 8 a.m. from the same point in opposite directions, how many times shall they cross each other before 9.30 a.m.?
Two boys starts from the same place walking at the rate of 5 kmph and 5.5 kmph respectively in the same direction. What time will they take to be 8.5 km apart?
In covering a distance of 30 km, Arun takes 2 hours more than Anil. If Arun doubles his speed, then he would take 1 hour less than Anil. What is Arun's speed?
A car travels first 160 km at 64 km/hr and the next 160 km at 80 km/hr. What is the average speed for the first 320 km of the tour?
A jeep travels a distance of 100 km at a uniform speed. If the speed of the jeep is 5 kmph more, then it takes 1 hour less to cover the same distance. The original speed of the jeep is:
Two athletes cover the same distance at the rate of 10 and 15 kmph respectively. Find the distance travelled when one takes 15 minutes longer than the other.
If Sita walks at 5 kmph, she misses her train by 10 minutes. If she walks at 7 kmph, she reaches the station 10 minutes early. How much distance does she walk to the station?
A person travelled 120 km by steamer, 450 km by train and 60 km by horse. It took him 13 hours 30 minutes. If the speed of the train is 3 times that of the horse and 1.5 times that of the steamer, then what is the speed (in km/h) of the steamer?
A train traveling at 100 kmph overtakes a motorbike traveling at 64 kmph in 40 seconds. What is the length of the train in meters?
Find the time taken by two trains, one 180 m long and the other 270 m long, to cross each other, if they are running at speeds of 46 kmph and 54 kmph respectively. Consider both possible cases of motion.
A distance is covered at a certain speed in a certain time. If the double of this distance is covered in four times the time, then what is the ratio of the two speeds?
Two men A and B walk from P to Q, a distance of 21 km, at 3 and 4 km an hour respectively. B reaches Q, returns immediately and meets A at R. The distance from P to R is
A ship is 156 km away from the bank of river. A leak, which admits 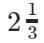 metric tons of water in
metric tons of water in 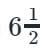 min, but the pumps throughout 15 metric tons in 1 hour. 68 metric tons would sufficient to sink the ship. Find the average rate of sailing so that she may just reach the bank as she begins to sink
min, but the pumps throughout 15 metric tons in 1 hour. 68 metric tons would sufficient to sink the ship. Find the average rate of sailing so that she may just reach the bank as she begins to sink
A train crosses a platform in 36 seconds and a pole in 12 seconds. If the length of the platform is 240 meters, what is the length of the train?

















