Test: Stress-Strain Relations & Elastic Constants - 1 - Mechanical Engineering MCQ
10 Questions MCQ Test Topicwise Question Bank for Mechanical Engineering - Test: Stress-Strain Relations & Elastic Constants - 1
The independent elastic constants for homogeneous and isotropic material are
For a linearly elastic, isotropic and homogeneous material, the number of elastic constants required to relate stress to strain is
If the Young’s modulus E is equal to bulk modulus K, then the value of Poisson’s ratio is
What will be the value of the Poisson’s ratio if the Youngs modulus E is equal to the bulk modulus K?
A 50 cm long x 20 cm diameter cylinder of brass was subjected to a tensile load of 0.1 MN. The resulting increase in length and decrease in diameter were noted 1 mm and 0.1 mm respectively. Then the brass has a Poisson’s ratio equal to
Consider a bar of length L, breadth B and thickness t subjeced to an axial pull or tension P. The resulting volumetric strain will be equal to
If E, G and K denote the Young’s modulus, modulus of rigidity and bulk modulus for an elastic material, then which one of the following can be possibly true?
A spherical ball of 0.5 x 103 mm3 volume is subjected to a volumetric stress of 0.5 MPa. If bulk modulus of the bail material is 16 GPa, the change in volume of the ball would be approximately equal to
For an isotropic, homogeneous and elastic material obeying Hooke’s law, number of independent elastic constants are
The number of elastic constants for a completely anisotropic elastic material are
|
45 videos|314 tests
|



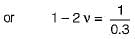 (∴ E = K)
(∴ E = K)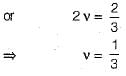
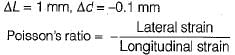
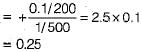

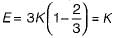 (Possible relation)
(Possible relation)

















