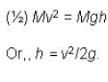Test: Rolling Motion - JEE MCQ
10 Questions MCQ Test - Test: Rolling Motion
A spherical solid ball rolls on a table. What fraction of its total K.E. is rotational K.E. ?
A body is rolling down an inclined plane without slipping. How does the acceleration of the rolling body depend on its radius?
Acceleration (a) of a body of radius R rolling down an inclined plane of inclination is given by
What is the moment of inertia of a solid sphere about its diameter?
What is the coefficient of friction when a cylinder rolls down without slipping on an inclined plane?
If a solid cylinder rolls up along a inclined plane with an initial velocity v. It will rise up to a height h equal to
What will be the speed of center of mass, if a solid sphere of radius 20 cm which rotates at 2 rps along a straight line?
Two discs A and B are mounted on a vertical axle. Suppose the discs have moment of inertia as I and 2 I respectively about an axis. Disc A is given angular velocity ω, using the potential energy of a spring compressed by x1. Similarly the potential energy of a spring compressed by x2 gives an angular velocity of 2ω to Disc B. Considering that both the discs rotate in same direction .Find the ratio x1/ x2 :
A small cylinder rolling with a velocity v along a horizontal surface encounters a smooth inclined surface. The height ‘h’ up to which the cylinder will ascend is