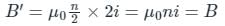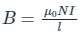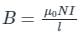Test: Solenoid - JEE MCQ
10 Questions MCQ Test - Test: Solenoid
The force between two current carrying conductors is due to which of the following
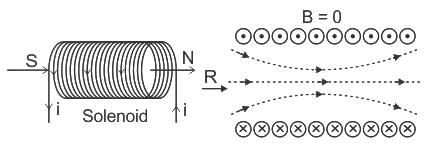
A solenoid coil of 300 turns /m is carrying a current of 5 A. Calculate the magnitude of magnetic intensity inside the solenoid.
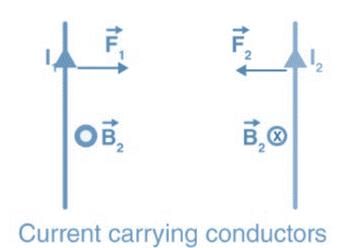
There is a very long, very tightly wound solenoid in a round tube shape of small radius (compared to its length). It carries constant electric current. Now, it is bend to form a closed toroid. Consider the magnetic field inside the tube. It will
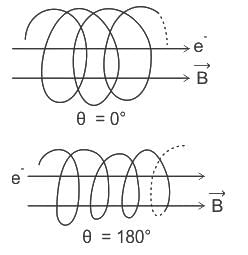
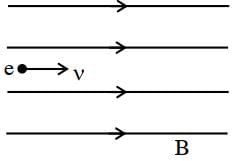
An electron is projected with uniform velocity along the axis of a current carrying long solenoid. Which of the following is true?
A long solenoid carrying a current produces a magnetic field B along its axis. If the current is doubled and the number of turns per cm is halved, the new value of magnetic field will be equal to
An electron is projected with uniform velocity along the axis inside a current carrying long solenoid. Then :
Consider a long solenoid of 'n' turns per unit length and carrying a current 'I'. The magnetic field in the interior of the solenoid was shown to be given
by Bo= ___________.



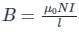
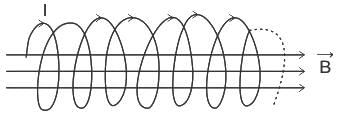
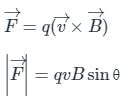
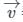 = velocity vector of the electron
= velocity vector of the electron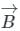 = magnetic field
= magnetic field