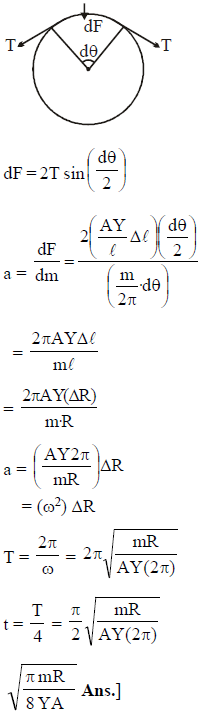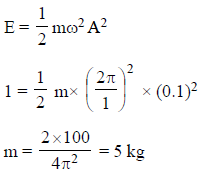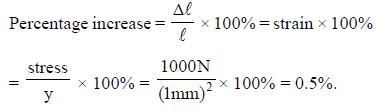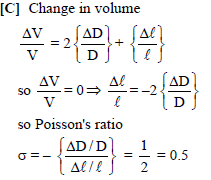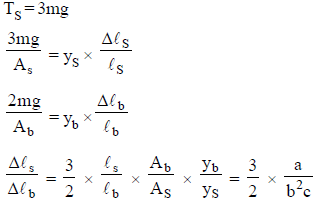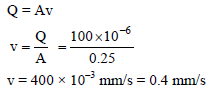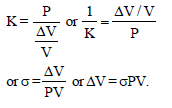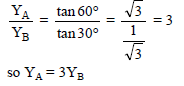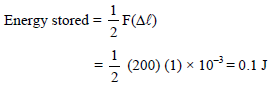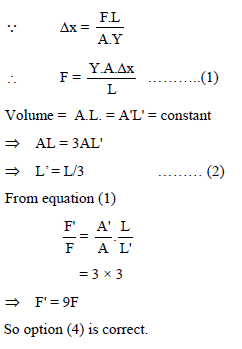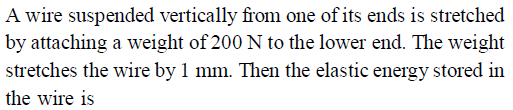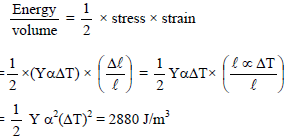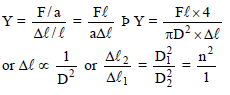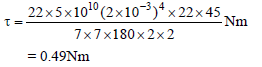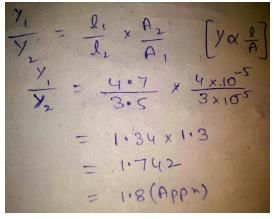Chapter Test: Elasticity (Mechanical Properties of Solids) - 2 - JEE MCQ
30 Questions MCQ Test - Chapter Test: Elasticity (Mechanical Properties of Solids) - 2
The young's modulus of material of a thin ring shaped elastic body is Y. The mass of ring is m, area of cross section is A, It's initial radius is R. Ring is a little elongated, then left alone. At what time will ring circumference be same as it was initially. Neglect loss of energy.
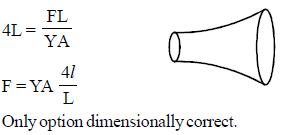
A slightly conical wire of length L and end radii r1 and r2 is stretched by two forces F, F applied parallel to length in opposite directions and normal to end faces. If Y denotes the Young’s modulus, then extension produced is
A block is executing SHM with a time period of 1 sec. and energy of 1 J. What is the mass (in kg) of the block? The amplitude is 10 cm. (Take π2 = 10)

A steel wire (Y = 200 GPa) of cross-sectional area = 1 mm2 is stretched by a force = 1000 N. The percentage increases in length of the wire is
A wire of length '2m' is clamped horizontally between two fixed support. A mass m = 5 kg is hanged from middle of wire. The vertical depression in wire in equilibrium is (young modulus of wire = 2.4 × 109 N/m2, crosssectional area = 1 cm2) -
If there is no change in the volume of wire on stretching, then poisson's ratio for the material of wire is -
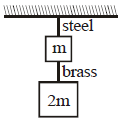
If the ratio of lengths, radii and Young’s moduli of steel and brass wires in the figure are a,b and c respectively, then the corresponding ratio of increase in their lengths is
Blood is flowing at the rate of 100 cm3/s in a capillary of cross sectional area 0.25 m2. The velocity of flow is -
If the compressibility of water is σ per unit atmospheric pressure, then the decrease in volume (V) due to atmospheric pressure P will be -
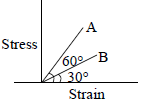
The stress versus strain graphs for wires of two materials A and B as shown is the figure. If YA and YB are the young’s modulus of the materials, then-
A wire suspended vertically from one of its ends is stretched by attaching a weight of 200N to the lower end. The weight stretches the wire by 1mm. Then the elastic energy stored in the wire-
Two wires are made of the same material and have the same volume. However wire 1 has cross-sectional area A and wire 2 has crosssectional area 3A. if the length of wire 1 increases by Δx on applying force F, how much force is needed to stretch wire 2 by the same amount ?
Two wires of the same radius and material and having lengths in the ratio 8.9 : 7.6 are stretched by the same force. The strains produced in the two cases will be in the ratio -
A uniform metal rod of 2 mm2 cross section is heated from 0ºC to 20ºC. The coefficient of linear expansion of the rod is 12 × 10–6/ºC, its Young's modulus is 1011 N/m2. The energy stored per unit volume of the rod is -
The ratio of diameters of two wires of same material in n : 1. The length of each wire is 4m. on applying the same load, the increase in length of thin wire will be (n > 1) -
A metal rod of Young's modulus 2 × 1010 Nm–2 undergoes an elastic strain of 0.06%. The energy per unit volume stored in J m–3 is -
In order to twist one end of a wire, 2m long and 4 mm in diameter, though 45º, the torque required is -(η = 5 × 1010 Nm–2)
Two wires of the same radius and material have their length in the ratio 1 : 2. If these are stretched by same force and strain produced in the two wires will be in the ratio -
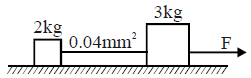
Two bodies of masses 2kg and 3kg are connected by a metal wire of cross section 0.04 mm2. Breaking stress of metal wire is 2.5 GPa. The maximum force F that can be applied to 3kg block so that wire does not break is : (Neglect friction)
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire were twice as long?
Columns are loaded in
The S.I unit of stress is
Material is said to be ductile if
In constructing a large mobile, an artist hangs an aluminum sphere of mass 6.0 kg from a vertical steel wire 0.50 m long and 2.5 × 10−3 cm2in cross-sectional area. On the bottom of the sphere he attaches a similar steel wire, from which he hangs a brass cube of mass 10.0 kg. Compute the elongation.
volume strain is defined
A steel wire of length 4.7 m and cross-sectional area 3.0 × 10−5 m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0 × 10−5 m2 under a given load. What is the ratio of the Young’s modulus of steel to that of copper?