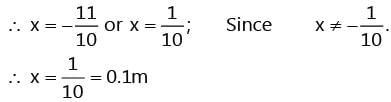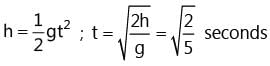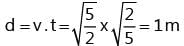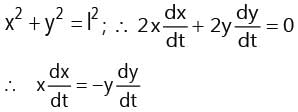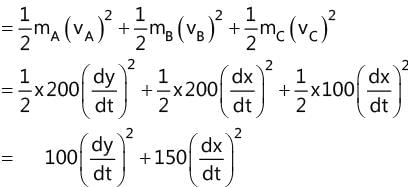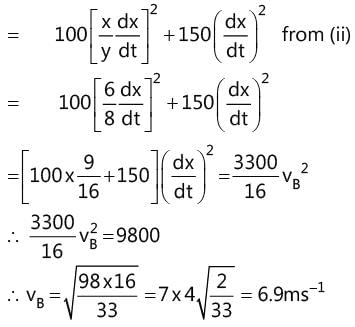HC Verma Test: Work, Energy & Power - NEET MCQ
25 Questions MCQ Test Topic-wise MCQ Tests for NEET - HC Verma Test: Work, Energy & Power
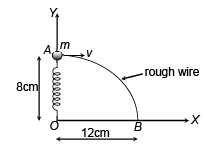
A ring of mass 200 gram is attached to one end of a light spring of force constant 100 N/m and natural length 10 cm. The ring is constrained to move on a rough wire in the shape of the quarter ellipse of the major axis 24 cm and the minor axis 16 cm with its centre at the origin. The plane of the ellipse is vertical and wire is fixed at points A and B as shown in the figure. Initially, ring is at A with other end of the spring fixed at the origin. If normal reaction of wire on ring at A is zero and ring is given a horizontal velocity of 10 m/s towards right so that it just reaches point B, then select the correct alternative (s) (g = 10 m/s2)
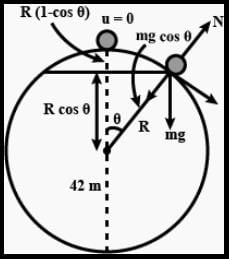
A particle is kept at rest at the top of a sphere of diameter 42 m. When disturbed slightly, it slides down. At what height h from the bottom, the particle will leave the sphere?
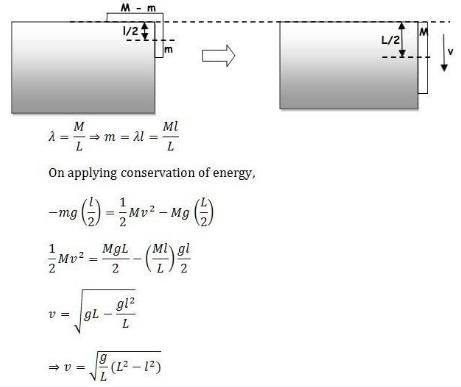
A uniform chain has a mass M and length L. It is placed on a frictionless table with length l0 hanging over the edge. The chain begins to slide down. The speed V with which the chain slides away from the edge is given by:
A particle is dropped from a height h. A constant horizontal velocity is given to the particle.
Taking g to be constant every where, kinetic energy E of the particle with respect to time t is correctly shown in
A particle moves on a rough horizontal ground with some initial velocity say v0. If (3/4)th of its kinetic energy is lost due to friction in time t0 then coefficient of friction between the particle and the ground is
A block weighing 10 N travels down a smooth curved track AB joined to a rough horizontal surface (figure). The rough surface has a friction coefficient of 0.20 with the block. If the block starts slipping on the track from a point 1.0 m above the horizontal surface, the distance it will moves on the rough surface is
A wedge of mass M is fitted with a spring of stiffness ‘k’ is kept on a smooth horizontal surface. A rod of mass m is kept on the wedge as shown in the figure. System is in equilibrium.
Assuming that all surfaces are smooth, the potential energy stored in the spring is:
The potential energy of a particle varies with a distance x as shown in the graph.The force acting on the particle is zero at
The ends of a spring are attached to blocks of masses 3 kg and 2 kg. The 3 kg block rests on a horizontal surface and the 2 kg block which is vertically above it is in equilibrium producing a compression of 1 cm of the spring. The value of the length to which the 2 kg mass must be compressed, so that when it is released, the 3 kg block may be lifted off the ground is:
A body of mass m accelerates uniformly from rest to a speed v0 in time t0 . The work done on the body till any time t is
An inclined plane ends into a vertical loop of radius r as shown in figure. If a particle of mass m is released from topmost point. The point C on the track as shown in the figure and centre of circular track are at same horizontal level. The normal force at point C is
A uniform rod of length L and mass M is placed on a rough horizontal surface. The force F applied on the rod is such that the rod is just in the state of rest. If the coefficient of friction varies according to the relation μ = KX, where K is a positive constant. Suppose friction is present only from X = 0 to X = L. If the rod moves in the direction of application of force then the total heat generated in the time in which the rod crosses this region, is equal to
In the figure shown all the surfaces are frictionless, and mass of the block, m = 1 kg. The block and wedge are held initially at rest. Now wedge is given a horizontal acceleration of 10 m/s2 by applying a force on the wedge, so that the block does not slip on the wedge. Then work done by the normal force in ground frame on the block in √3 seconds is
Suppose potential energy between particle A and B at separation r is given by U = k ln r, where k is constant. For such hypothetical system, the ratio of energy difference between energy levels (n = 1 and n = 2) and (n = 2 and n = 4) is (The energy of a particle in nth level is –13.6/n2)
A 1.0 kg block collides with a horizontal weightless spring of force constant 2.75 Nm−1 as shown in figure. The block compresses the spring 4.0 m from the rest position. If the coefficient of kinetic friction between the block and horizontal surface is 0.25, the speed of the block at the instant of collision is
Three blocks A, B and C are kept as shown in figure. The coefficient of friction between A and B is 0.2, B and C is 0.1, C and ground is 0.0. The mass of A, B and C are 3 kg, 2 kg and 1 kg respectively. A is given a horizontal velocity 10 m/s. A, B and C always remain in contact i.e. lies as in figure. The total work done by friction will be
A block of mass m is placed inside a smooth hollow cylinder of radius R kept horizontally.Initially system was at rest. Now cylinder is given constant acceleration 2 g in the horizontal direction by external agent. The maximum angular displacement of the block with the vertical is:
Two point masses of mass 4 m and m respectively separated by a distance d are revolving under mutual force of attraction. Ratio of their kinetic energy will be
When an object is allowed to slide down a hill it stops at the point B because of friction. If friction force depends only on the normal component of the reaction force with coefficient of friction variable along the path, the work done in taking the object slowly from B to A along the hill will be
If the heart pushes 1 cc of blood in 1 s under pressure 20000 Nm-2, the power of the heart is
An object of mass 5 kg falls from rest through a vertical distance of 20 m and attains a velocity of 10 m/s. How much work is done by the resistance of the air on the object? (g = 10 m/s²)
A 0.5 kg block slides from the point A on a horizontal track with an initial speed of 3 m/s toward a weightless horizontal spring of length 1 m and force constant 2 N/m. The part AB of the track is frictionless and the part BC has the coefficients of static and kinetic friction as 0.22 and 0.2, respectively. If the distances AB and BD are 2 m and 2.14 m, respectively find the total distance through which the block moves before it comes to rest completely (Take g = 10 m/s2).
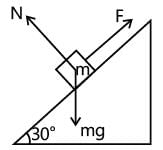
A block of mass 2 kg is pulled up on a smooth incline of angle 30o with horizontal. If the block moves with an acceleration of 1m/s2, find the power delivered by the pulling force at a time t = 4 s after motion starts. What is the average power delivered during these four seconds after the motion starts?
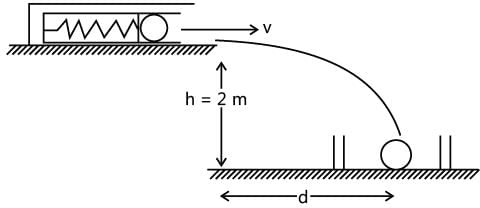
In a spring gun having spring constant 100 N/m, a small ball of mass 0.1 kg is put in its barrel by compressing the spring through 0.05 m as shown in the Fig. 5.29. Find where a box should be placed on the ground so that ball falls in it, if the ball leaves the gun horizontally at a height of 2 m above the ground? (g = 10 m/s2).
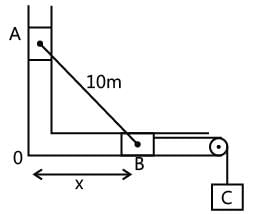
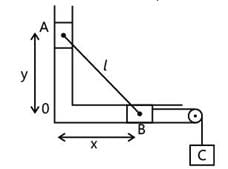
Two bodies A and B connected by a light rigid bar of 10 m long move in two frictionless guides as shown in the Figure. If B starts from rest when it is vertically below A, find the velocity of B when X = 6 m.
|
9 docs|1256 tests
|


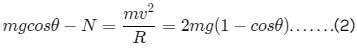

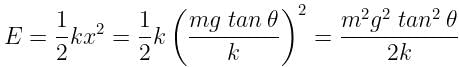

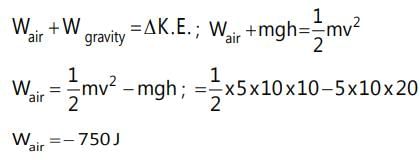
 ....(i)
....(i)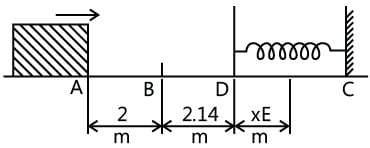
 ...(iii)
...(iii)