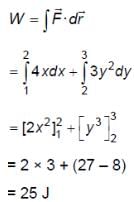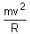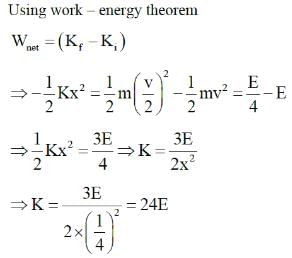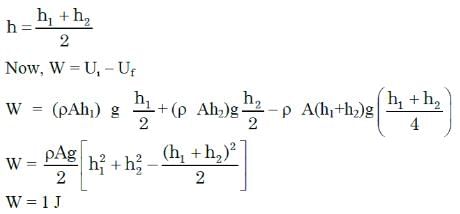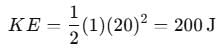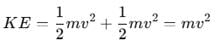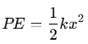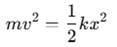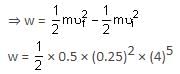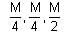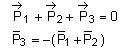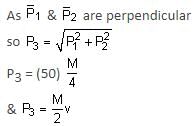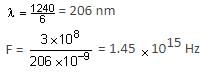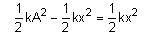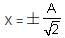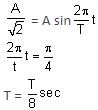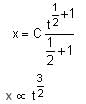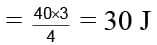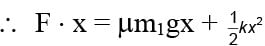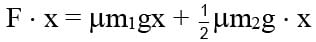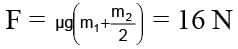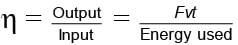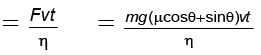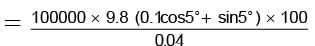Test: Work, Energy & Power - 1 - NEET MCQ
25 Questions MCQ Test Physics Class 11 - Test: Work, Energy & Power - 1
A particle experiences a variable force 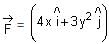 in a horizontal x-y plane. Assume distance in meters and force in newton. If the particle moves from point (1, 2) to point (2, 3) in the x-y plane; then kinetic energy changes by
in a horizontal x-y plane. Assume distance in meters and force in newton. If the particle moves from point (1, 2) to point (2, 3) in the x-y plane; then kinetic energy changes by
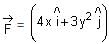 in a horizontal x-y plane. Assume distance in meters and force in newton. If the particle moves from point (1, 2) to point (2, 3) in the x-y plane; then kinetic energy changes by
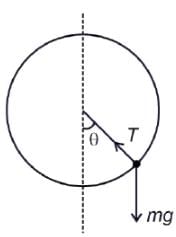
in a horizontal x-y plane. Assume distance in meters and force in newton. If the particle moves from point (1, 2) to point (2, 3) in the x-y plane; then kinetic energy changes byA stone of mass m tied to a string is being whirled in a vertical circle with a uniform speed. The tension in the string is
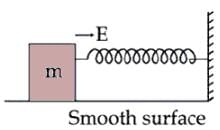
A block of mass 'm' (as shown in figure) moving with kinetic energy E compresses a spring through a distance 25 cm when its speed is halved. The value of spring constant of used spring will be nE Nm-1 for n = _____________. (in integers)

Two cylindrical vessels of equal cross-sectional area 16 cm2 contain water up to heights 100 cm and 150 cm, respectively. The vessels are interconnected so that the water levels in them become equal. The work done by the force of gravity during the process is: [Take density of water = 103 kg/m3 and g = 10 ms-2]
A body of mass 1 kg is thrown upwards with a velocity 20m/s. It momentarily comes to rest after attaining a height of 18 m. How much energy is lost due to air friction?
( g=10m/s2 ):
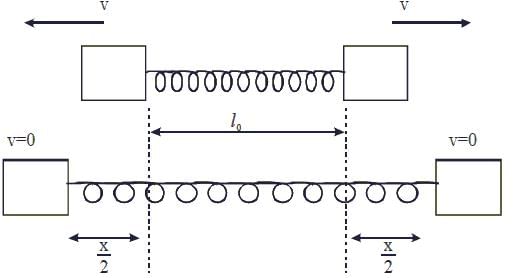
As per the given figure, two blocks each of mass 250 g are connected to a spring of spring constant 2 Nm-1. If both are given velocity v in opposite directions, then maximum elongation of the spring is:

A body of mass 0.5 kg travels on a straight line path with velocity v = (3x2 + 4) m/s. The net work done by the force during its displacement from x = 0 to x = 2 m is:
A particle of mass 500 gm is moving in a straight line with velocity v = b x5/2. The work done by the net force during its displacement from x = 0 to x = 4 m is: (Take b = 0.25 m-3/2 s-1)
A body of mass M at rest explodes into three pieces, in the ratio of masses 1 : 1 : 2. Two smaller pieces fly off perpendicular to each other with velocities of 30 ms-1 and 40 ms-1 respectively. The velocity of the third piece will be:
A free electron of 2.6 eV energy collides with a H+ ion. This results in the formation of a hydrogen atom in the first excited state and a photon is released. Find the frequency of the emitted photon (h = 6.6 × 10-34 J s).
A particle of mass 1 kg is hanging from a spring of force constant 100 Nm-1. The mass is pulled slightly downward and released, so that it executes free simple harmonic motion with time period T. The time when the kinetic energy and potential energy of the system will become equal is 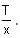 The value of x is _______. (in integers)
The value of x is _______. (in integers)
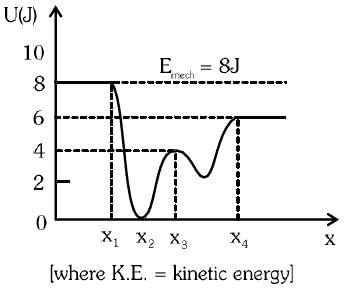
Given below is the plot of a potential energy function U(x) for a system, in which a particle is in one dimensional motion, while a conservative force F(x) acts on it. Suppose that Emech = 8 J, the incorrect statement for this system is:
A body at rest is moved along a horizontal straight line by a machine delivering a constant power. The distance moved by the body in time 't' is proportional to
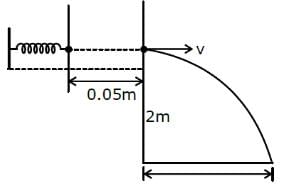
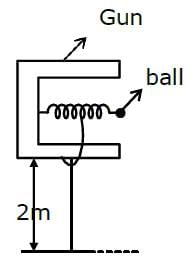
In a spring gun having spring constant 100 N/m, a small ball 'B' of mass 100 g is put in its barrel (as shown in figure) by compressing the spring through 0.05 m. There should be a box placed at a distance 'd' on the ground so that the ball falls in it. If the ball leaves the gun horizontally at a height of 2 m above the ground, the value of d is _______________ m.
(g = 10 m/s2) (in integers)
A 60 HP electric motor lifts an elevator having a maximum total load capacity of 2000 kg. If the frictional force on the elevator is 4000 N, the speed of the elevator at full load is close to: (1 HP = 746 W, g = 10 ms-2)
Physically, the notion of potential energy is applicable only to
A bolt of mass 0.3 kg falls from the ceiling of an elevator moving down with an uniform speed of 7 m/s. It hits the floor of the elevator (length of the elevator = 3 m) and does not rebound. What is the heat produced by the impact?
A 50.0-kg marathon runner runs up the stairs to the top of a 443-m-tall Tower. To lift herself to the top in 15.0 minutes, what must be her average power output?
The launching mechanism of a toy gun consists of a spring of unknown spring constant. When the spring is compressed 0.120 m, the gun, when fired vertically, is able to launch a 35.0-g projectile to a maximum height of 20.0 m above the position of the projectile before firing. Neglecting all resistive forces, determine the spring constant.
A body is projected at an angle of 30° to the horizontal with kinetic energy 40 J. What will be the kinetic energy at the top most point?
A body is slowly lowered on to a massive platform moving horizontally at a speed of 4 m/s. through what distance will the body slide relative to the platform? (The coefficient of friction is 0.2; g = 10 m/s2)
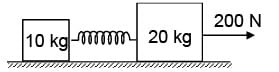
Two masses 10 kg and 20 kg are connected by a massless spring. A force of 200 N acts on 20 kg mass. At the instant when the 10 kg mass has an acceleration 12 m/s2 the energy stored in the spring (k = 2400 N/m) will be
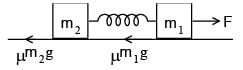
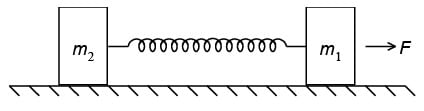
Two bars of masses m1 = 4 kg and m2 = 8kg connected by a non-deformed light spring rest on a horizontal plane. The coefficient of friction between bars and surface is μ = 0.2. What minimum constant force has to be applied in the horizontal direction to the bar of mass m1 in order to shift the other bar?
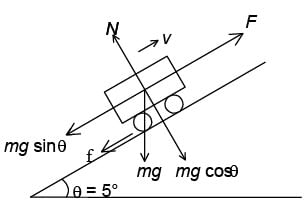
A 100000 kg engine is moving up a slope of gradient 5o at a speed of 100 m/hr. The coefficient of friction between the engine and the rails is 0.1. If the engine has an efficiency of 4% for converting heat into work, find the amount of coal, the engine has to burn up in one hour. (Burning of 1 kg of coal yields 50000 J.)
|
97 videos|379 docs|103 tests
|