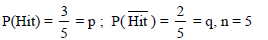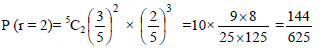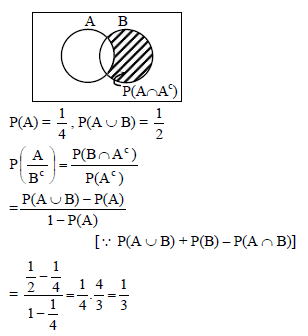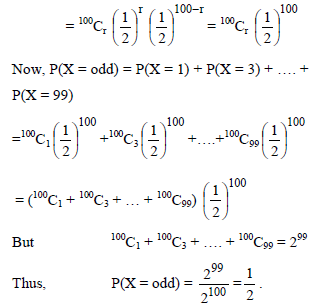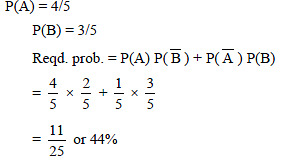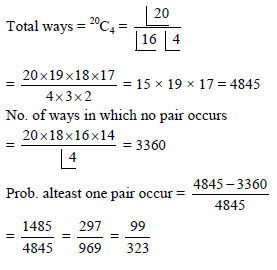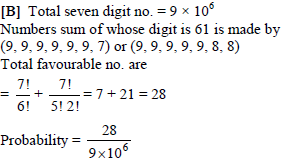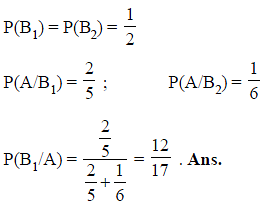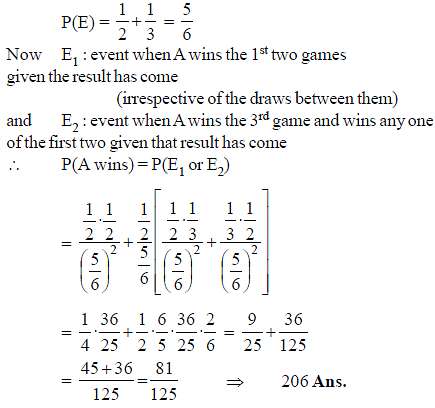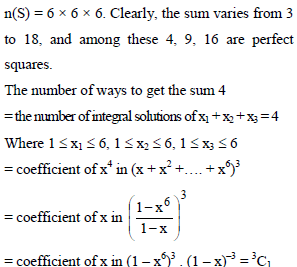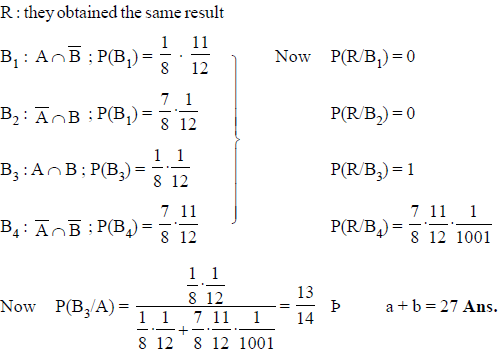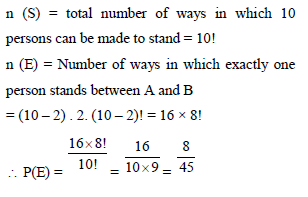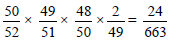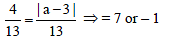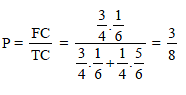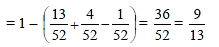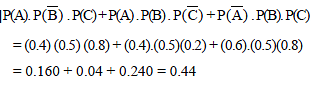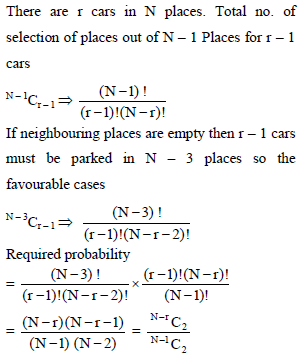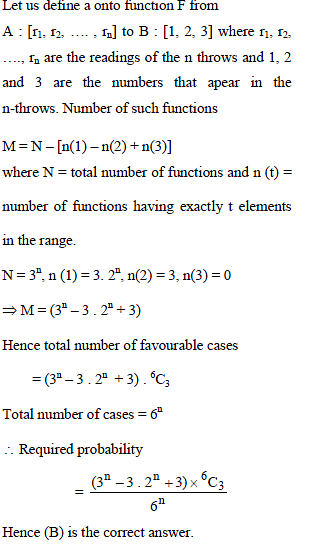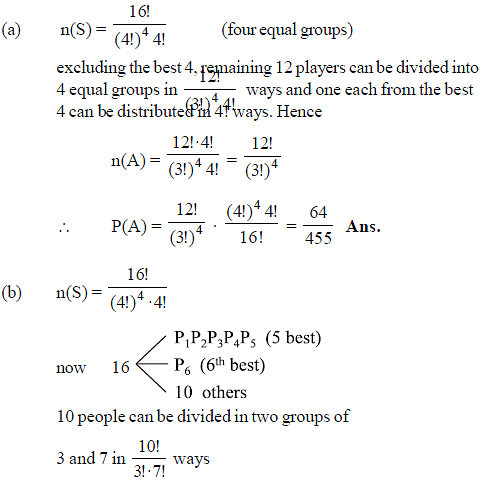Probability - 2 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Probability - 2
A man make attempts to hit the target. The probability of hitting that target is 3/5 . Then the probability that A hit the target exactly 2 times in 5 attempts, is -
Consider a set 'P' containing 'n' elements. A subset 'A' of 'P' is drawn and there after set 'P' is reconstructed. Now one more subset 'B' of 'P' is drawn. Probability of drawing sets A and B so that A ∩B has exactly one element –
A fair coin is tossed 100 times. The probability of getting tails an odd number of times is-
A speaks truth in 80% cases and B in 60% cases. In what percentage of case are they likely to contradict each other in starting the same fact :
There are 10 pairs of shoes in a cupboard from which 4 shoes are picked at radndom. The probability that there is at least one pair is
Four numbers are multiplied together. Then the probability that the product will be divisible by 5 or 10 is -
Seven digit numbers are made from using all digits repetition of digits is allowed. Then the probability that the sum of digits of number is 61, is
A letter has either come from LONDON or CLIFTON, but on the post mark 2 consecutive letters 'ON' are found to be visible. The probability that the letter has come from LONDON is
A match between two players A and B is won by the player who first wins two games. A's chance of winning, drawing or losing any particular games are 1/2, 1/6 or 1/3 respectively. If the probability of A's winning the match can be expressed in the form p/q, find (p + q).
Three six-faced dice are thrown together. The probability that the sum of the numbers appearing on the dice is k (9 ≤ k ≤ 14), is -
Three dice are thrown. The probability of getting a sum which is a perfact square, is -
A, B are two inaccurate arithmeticians whose chance of solving a given question correctly are (1/8) and (1/12) respectively. They solve a problem and obtained the same result. If it is 1000 to 1 against their making the same mistake. If the chance that the result is correct is expressed as a/b , find the least value of (a + b).
There are 10 persons among whom are A and B who are made to stand in a row in random order. The probability that there is exactly one person between A and B is-
From a well shuffled pack of 52 playing cards, if cards are drawn one by one without replacement till the black ace comes, then probability that the black aces comes in the 4th draw is -
A man is known to speak truth in 75% cases. He throws a dice & reports that it is a six. The probability that it is actually a six is -
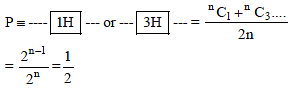
A coin is tossed ‘n’ times. The probability that head will turn up an odd no. of times is :
A card is drawn at random from a pack of 52 cards. The probability of drawing a card which is neither a heart nor a king is-
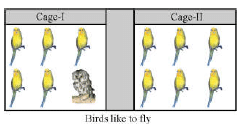
Shalu bought two cages of birds : Cage-I contains 5 parrots and 1 owl, and Cage-II contains 6 parrots, as shown.
One day Shalu forgot to lock both cages and two birds flew from Cage-I to Cage-II. Then two birds flew back from Cage-II to Cage-I. Assume that all birds have equal chance of flying, the probability that the Owl is still in Cage-I, is
Three rifle man take one shot each at the same target. The probability of the first rifle man hitting the target is 0.4, the probability of the 2rd rifle man hitting target is 0.5 and the probability of third rifle man hitting the target is 0.8. Then the probability that exactly two of them hit the target is
A car is parked among N cars standing in a row, but not at either end. On his return, the owner finds that exactly 'r' of the N placed are still occupied. The probability that both the places neighbouring his car empty is -
From each of the four married couples, one of the partners is selected at random. The probability that those selected are of the same sex is-
In an hotel International, 40% English and 60% Americans people are staying. English and American spellings for the same word are 'RIGOUR' and 'RIGOR', respectively. A randomly chosen man staying at a Nigerian hotel writes this word, and a letter taken at random from his spelling was found to be a vowel. Then the probability that the writer is an Englishman, can be expressed as (p/q), p, q ∈ N, find the least value of (p + q).
Three critics review a book. Odds in favour of the book are 5 : 2, 4 : 3 and 3 : 4 respectively for the three critics. The probability that majority are in favour of the book is
An unbiased die, with faces numbered 1, 2, 3, 4, 5, 6, is thrown n times and the list of n numbers shown up is noted. Then the probability that, among the numbers 1, 2, 3, 4, 5, 6, only three numbers appear in this list, is -
A permutation of 5 digits from the set {1, 2, 3, 4, 5} where each digit is used exactly once, is chosen randomly. Let p/q expressed as rational in lowest form be the probability that the chosen permutation changes from increasing to decreasing, or decreasing to increasing at most once e.g. the strings like 1 2 3 4 5, 5 4 3 2 1, 1 2 5 4 3 and 5 3 2 1 4 are acceptable but strings like 1 3 2 4 5 or 5 3 2 4 1 are not, find (p + q).
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|