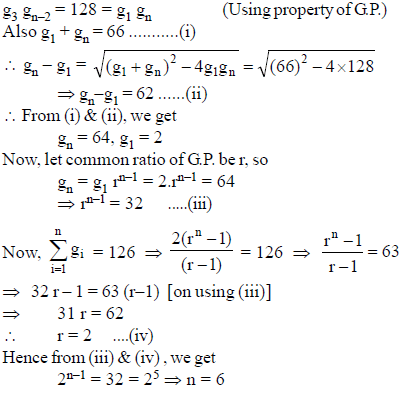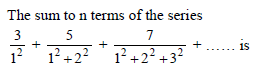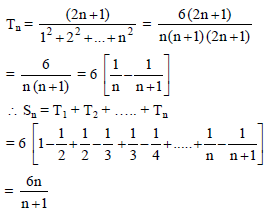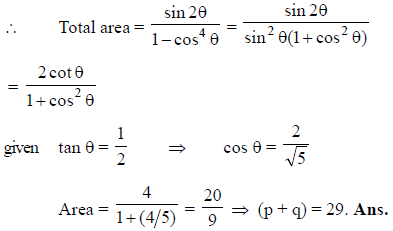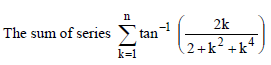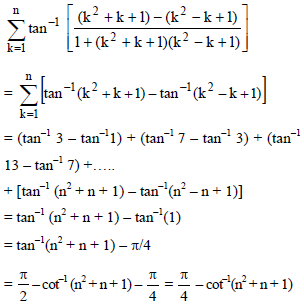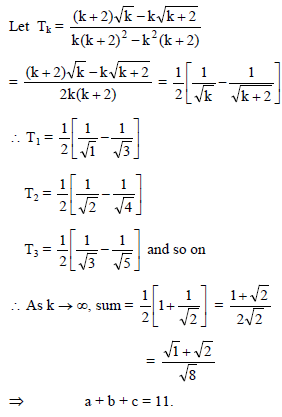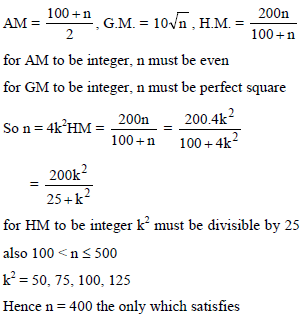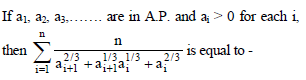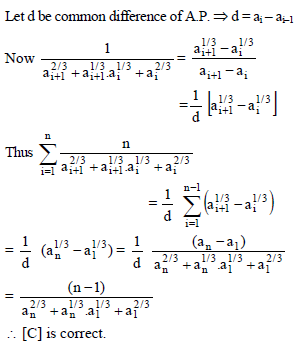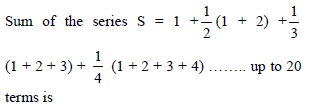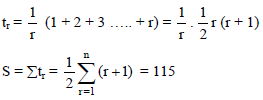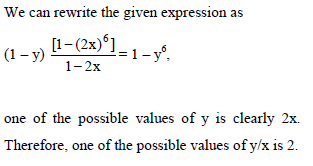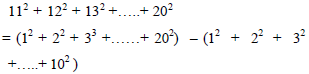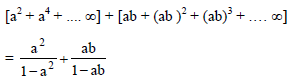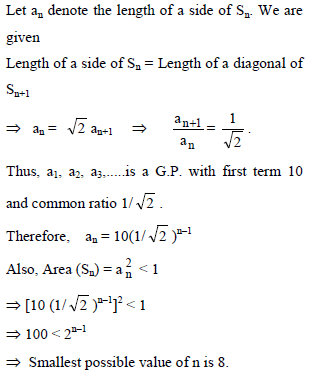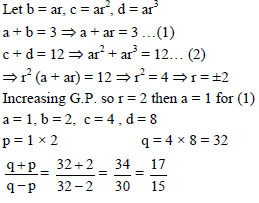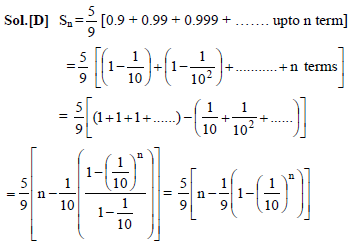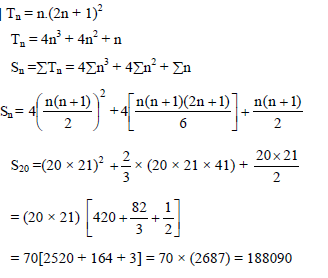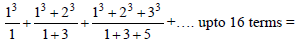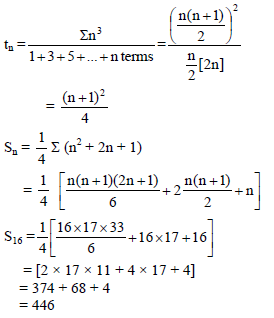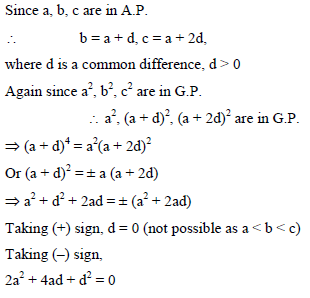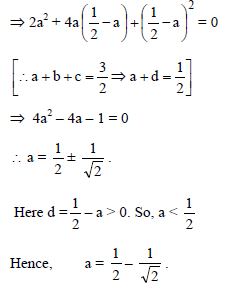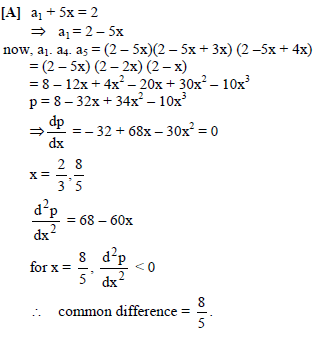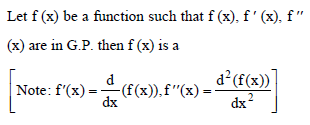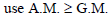Sequences and Series - 2 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Sequences and Series - 2
The right triangle ABC has legs of length AB = 2 and BC = 4. Point D is the foot of the perpendicular from B on the side AC. The altitude from D of triangle BDC meets the side BC at E. The altitude from E of triangle DEC meets DC at F......(as so forth). If the area of the shaded regions can be expressed in lowest rational equal to p/q , find (p + q).


If A.M., G.M. and H.M. of first and last terms of the series 100, 101, 102,…. n –1, n are the terms of the series it self then the value of n is (100 < n ≤ 500 )
If (1 – y) (1 + 2x + 4x2 + 8x3 + 16x4 + 32x5) = 1 – y6, (y ≠ 1), then a value y/x is -
If | a | <1 & | b | < 1 then sum of the series a (a + b) + a32 (a2+ b2) + a3 (a3+ b3) + ….. up to ∞ is
Consider an infinite G.P. with first term a and common ratio r. Its sum is 4 and the second term is 3/4, then
Let S1, S2,… be squares such that for each n ≥ 1, the length of a side of Sn equals the length of a diagonal of Sn+1. If the length of a side of S1 is 10 cm, then the smallest value of n for which Area (Sn) < 1 is -
Let a, b be the roots of x2 –3x + p = 0 and let c, d be the roots of x2 –12x + q = 0, where a, b, c, d form an increasing G.P. Then the ratio of q + p : q – p is equal to
Sum of the series .5 + .55 + .555 + ………. upto n terms is
Suppose a, b, c are in A.P. and a2, b2, c2 are in G.P. If a < b < c and a + b + c =3/2, then the value of a is -
If the sixth term of an A.P. is equal to 2. the value of the common difference of the A.P. which makes the product a1 a4 a5 the greatest is
(the ith term is denoted by a)
If x, y, z are positive nos. minimum value of xlny –lnz + ylnz–lnx + zlnx –lny is –
|
209 videos|467 docs|187 tests
|
|
209 videos|467 docs|187 tests
|