Test: Combinations - JEE MCQ
20 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Test: Combinations
In a college there are 20 professors including the principal and the vice principal. A committee of 5 is to be formed. In how many ways it can be formed so that neither the principal nor the vice principal is included?
What is the number of diagonals that can be drawn by joining the vertices of a hexagon?
Nidhi has 6 friends. In how many ways can she invite one or more of them to a party at her home?
What is the number of ways of choosing 6 cards from a pack of 52 playing cards?
In how many ways can a cricket team of 11 players selected out of 16 players if two particular players are to be included and one particular player is to be rejected?
In a room there are 2 green chairs, 3 yellow chairs and 4 blue chairs. In how many ways can Raj choose 3 chairs so that at least one yellow chair is included?
In how many ways can a student choose a programme of 5 courses if 9 courses are available and 2 courses are compulsory for every student.
A group consists of 4 girls and 7 boys. in how many ways a team of 5 members be selected consisting of 2 girls and 3 boys.
In how many ways can an examinee choose 5 questions out of 8 in a paper of Physics?
How many triangles can be formed by joining four points on a circle?
In how many ways can one select a cricket team of eleven from 13 players in which only 5 players can bowl. If each cricket team of 11 must include at least 4 bowlers.
A committee consists of 5 students 3 girls and 2 boys. If the team is to be formed out of 7 boys and 5 girls, then how many ways this selection can be made?
|
209 videos|447 docs|187 tests
|
|
209 videos|447 docs|187 tests
|



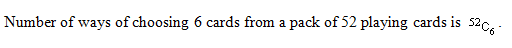
 = c. Find c.
= c. Find c.