Test: Equation Of Plane - JEE MCQ
10 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Equation Of Plane
The equation of the plane passing through the point (3, – 3, 1) and perpendicular to the line joining the points (3, 4, – 1) and (2, – 1, 5) is:
The equation of the plane, which is at a distance of 5 unit from the origin and has 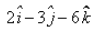 as a normal vector, is:
as a normal vector, is:
The length of the perpendicular from the origin to the plane 3x + 2y – 6z = 21 is:
If l, m, n are the direction cosines of the normal to the plane and p be the perpendicular distance of the plane from the origin, then the equation of the plane is:
If is the normal from the origin to the plane, and
is the unit vector along
. P(x, y, z) be any point on the plane and
is perpendicular to
. Then
The length of the perpendicular from the origin to the plane 2x – 3y + 6z = 21 is:
The angle between two lines whose direction ratios are 1,2,1 and 2,-3,4 is:
The equation of the plane passing through the points (2, 1, 0), (3, – 2, – 2) and (3, 1, 7) is:
|
204 videos|290 docs|139 tests
|




















