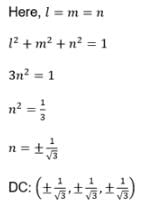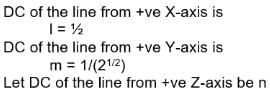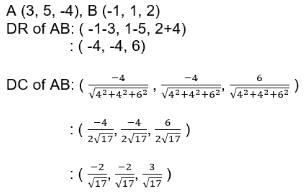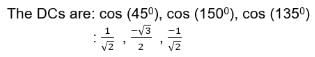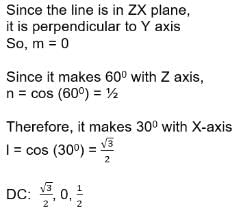Test: Introduction To 3D Geometry - JEE MCQ
20 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Introduction To 3D Geometry
Find the direction cosines of a line which makes equal angles with all three the coordinate axes.
Three planes, viz the XY Plane, XZ Plane and the YZ Plane divide the space into eight parts. Each part is called an OCTANT. What is the relation between these three planes
The co-ordinates of the vertices of the triangle are A(-2, 3, 6), B(-4, 4, 9) and C(0, 5, 8). The direction cosines of the median BE are:
If the direction cosines of a line from the positive X-axis and Y-axis areThe angle of the line through Z-axis is:
The direction cosines of the line equally inclined with the axes are:
The direction cosines of the line whose direction ratios are 6, – 6, 3 are:
The direction cosines of the line joining the points (2, -1, 8) and (-4, -3, 5) are:
Find the direction cosines of the side AB of the triangle whose vertices are A(3, 5, -4), B(-1, 1, 2) and C(-5, -5, -2)
If l, m , n are the direction cosines of any line, then sum of the squares of the direction cosines of the line is always
If a line has the direction ratios -4, 18, -12 then what are its direction cosines?
The direction cosines of the line equally inclined with the axes, are:
If a line makes angles 45°,150°, 135°, with x, y and z-axes respectively, find its direction cosines.
Find the equation of the set of points which are equidistant from the points (1, 2 , 3) and (3, 2, -1)
If a line in the ZX-plane makes an angle 60o with Z-axis, the direction cosines of this line are:
A line makes angles α, β, γ with the positive directions of X-axis, Y-axis and Z-axis, respectively, then the directions cosines of the line are:
The signs of the X,Y and Z coordinates of a point that lies in the octant OXYZ’ is
If a line in the ZX-plane makes an angle 30o with Z-axis, the direction cosines of this line are:
|
204 videos|290 docs|139 tests
|