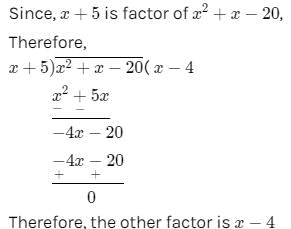Test: Introduction To Mathematical Induction - JEE MCQ
10 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - Test: Introduction To Mathematical Induction
If P(n) : (2n + 7) < (n + 3)2 then P(3) is
If P(n) is the statement; 4 + 8 + 12 +……+ 4n = 2n (n + 1) then P(6) will be
If 42x = 4-6 then what is the value of x ?
Assuming the truth of P(k) and proving P(k + 1) to be true, for some integer k is known as the _______ .
Every even power of an odd number greater than 1 when divided by 8 leaves 1 as the remainder.The inductive step for the above statement is
A set S in which x S implies x+1 S is known as a _______ .
If one of the factor of x2 + x – 20 is (x + 5). Find the other
If p(n) is the statement : 12 + 32 + 52 + __ __ + (2n - 1)2 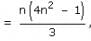 then which one of the following is incorrect?
then which one of the following is incorrect?
If a statement is to be proved by mathematical induction, then the different steps necessary to prove it are
In the principle of mathematical induction, which of the following steps is mandatory?
|
446 docs|930 tests
|