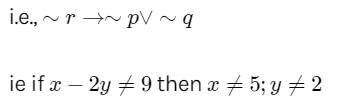Test: Mathematical Reasoning- 1 - JEE MCQ
25 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - Test: Mathematical Reasoning- 1
Let p and q be two propositions given by P : The sky is blue, q : Milk is white, Then , p^q is
Let p and q be two prepositions given by p : I play cricket during the holidays, q : I just sleep throughout the day then , the compound statement p ∧ q is
Let p and q be two prepositions given by p : It is hot, q : He wants water Then , the verbal meaning of p → q is
Let p and q be two prepositions given by p : I take medicine, q : I can sleep then ,the compound statement ∼p→∼q means
Which of the following is true for the propositions p and q ?
For any three propositions p, q, and r, the proposition (p∧q)∧(q∧r) is true, when
The negation of the proposition “if a quadrilateral is a square, then it is a rhombus “ is
The contrapositive of the statement “ if 22 = 5, then I get first class” is
If x = 5 and y = - 2, then x – 2y = 9. The contrapositive of this proposition is
Let p and q be two propositions. Then, the contrapositive of the implication p→q is
Which of the following statement is a tautology ?
Logical equivalent proposition to the proposition ∼(p∨q) is
Let p and q be two propositions. Then the implication p↔∼q is true ,when
Consider the proposition: “If we control population growth, we prosper “. Negative of this proposition is
Consider the proposition: “If the pressure increases, the volume decreases “. Negative of this proposition is
Which of the following connectives satisfy commutative law ?
Which of the following pairs is logically equivalent ?
|
446 docs|930 tests
|