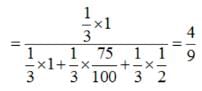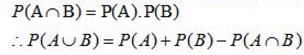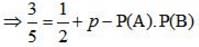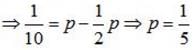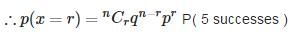Test: Probability - JEE MCQ
25 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Probability
The conditional probability of an event E, given the occurrence of the event F is given by
A coin is tossed three times, if E : head on third toss , F : heads on first two tosses. Find P(E|F)
Two cards are drawn at random and without replacement from a pack of 52 playing cards. Find the probability that both the cards are black.
A laboratory blood test is 99% effective in detecting a certain disease when it is in fact, present. However, the test also yields a false positive result for 0.5% of the healthy person tested (i.e. if a healthy person is tested, then, with probability 0.005, the test will imply he has the disease). If 0.1 percent of the population actually has the disease, what is the probability that a person has the disease given that his test result is positive?
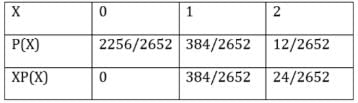
Suppose that two cards are drawn at random from a deck of cards. Let X be the number of aces obtained. Then the value of E(X) is
The conditional probability of an event E, given the occurrence of the event F
A coin is tossed three times, if E : at least two heads , F : at most two heads. Find P(E|F)
A box of oranges is inspected by examining three randomly selected oranges drawn without replacement. If all the three oranges are good, the box is approved for sale, otherwise, it is rejected. Find the probability that a box containing 15 oranges out of which 12 are good and 3 are bad ones will be approved for sale.
There are three coins. One is a two headed coin (having head on both faces),another is a biased coin that comes up heads 75% of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows heads, what is the probability that it was the two headed coin ?
The conditional probability of an event E’s complement E’, given the occurrence of the event F
A coin is tossed three times, E : at most two tails , F : at least one tail. Find P(E|F)
Given that the events A and B are such that P(A) = 1/2 , P (A ∪ B) = 3/5 and P(B) = p. Find p if they are mutually exclusive
An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probability of an accidents are 0.01, 0.03 and 0.15 respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver?
A black and a red dice are rolled. Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5.
Given that the events A and B are such that P(A) = 1/2 P (A ∪ B) = 3/5 and P(B) = p. Find p if they independent.
A random variable is a real valued function whose domain is the.
A die is thrown 6 times. If ‘getting an odd number’ is a success, what is the probability of 5 successes?
A black and a red dice are rolled. Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.
Let A and B be independent events with P (A) = 0.3 and P(B) = 0.4. Find P(A ∩ B)
Let X be a random variable assuming values x1, x2,....,xn with probabilities p1, p2, ...,pn, respectively such that . Mean of X denoted by μ is defined as
A die is thrown 6 times. If ‘getting an odd number’ is a success, what is the probability of at least 5 successes?
|
204 videos|290 docs|139 tests
|



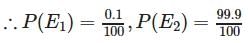 Let A = event that the test result is positive
Let A = event that the test result is positive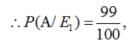
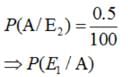

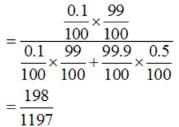
 Let A = event of getting head.
Let A = event of getting head.