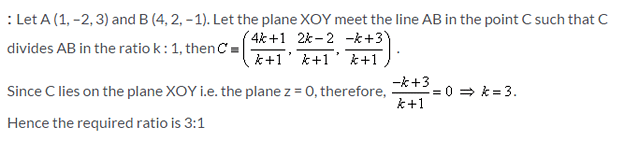Test: Section Formula 3D Geometry - Commerce MCQ
10 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Section Formula 3D Geometry
The coordinates of the centroid of a triangle whose vertices are (2, –1, 6), (3, 3, –2) and (–2, 1, –1) are:
The ratio, in which YZ-plane divides the line joining (2, 4, 5) and (3, 5, 7) is
The ratio in which the join of points (1, –2, 3) and (4, 2, –1) is divided by XOY plane is:
Three vertices of a parallelogram PQRS are P(3, – 1, 2), Q (1, 2, – 4) and R (- 1, 1, 2). Find the coordinates of the fourth vertex.
A point R with x-coordinate 1 lies on the line segment joining the points P(-2, 3,5) and Q (7, 0, -1). The coordinates of the point R are
If the origin is the centroid of the triangle ABC with vertices A (2a, 14, 6), B (8, 3b, -10) and C(-4, 2, 2c), then the values of a and c are.
If the origin is the centroid of the triangle PQR with vertices P(2a, 2, 6), Q(-4, 3b, -10) and (8, 14, 2c), then the values of a, b and c are:
The ratio in which the join of points (1, –2, 3) and (4, 2, –1) is divided by XOY plane is:
The coordinates of the point R which divides the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) externally in the ratio m : n are given by
The ratio in which the line joining the points (1, 2, 3) and (-3.4, -5) is divided by the xy-plane is:
|
75 videos|238 docs|91 tests
|