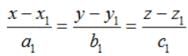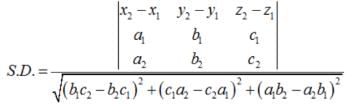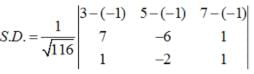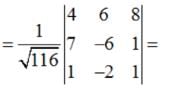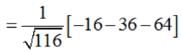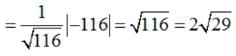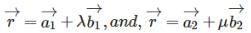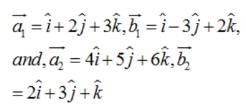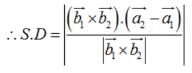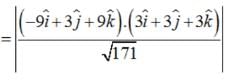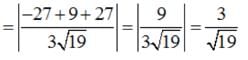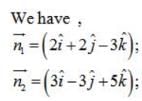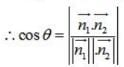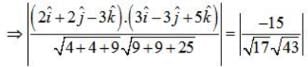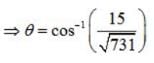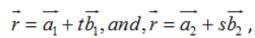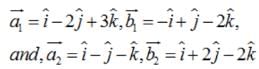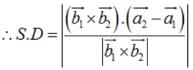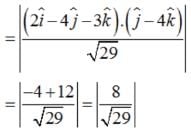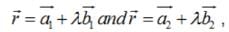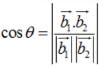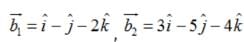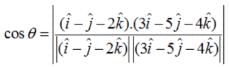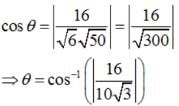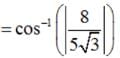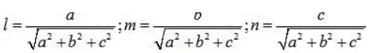Test: Three Dimensional Geometry- 1 - JEE MCQ
25 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Three Dimensional Geometry- 1
The angle θ between the planes A1x + B1y + C1z + D1 = 0 and A2 x + B2 y + C2 z + D2 = 0 is given by
Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0.
If l, m, n are the direction cosines of a line, then
Find the shortest distance between the lines :
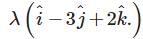
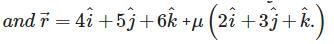
The distance of a point whose position vector is from the plane
Find the angle between the planes whose vector equations are
is a vector joining two points P(x1, y1, z1) and Q(x2, y2, z2). If
Direction cosines of
are
Find the shortest distance between the lines 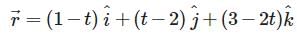 and
and 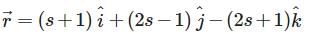
The distance d from a point P(x1, y1, z1) to the plane Ax + By + Cz + D = 0 is
Determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.7x + 5y + 6z + 30 = 0 and 3x – y – 10z + 4 = 0
If l, m and n are the direction cosines of a line, Direction ratios of the line are the numbers which are
Find the angle between the following pairs of lines:
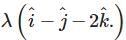 and
and 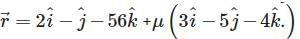
Determine the direction cosines of the normal to the plane and the distance from the origin. Plane z = 2
In the following case, determine whether the given planes are parallel orperpendicular, and in case they are neither, find the angles between them. 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0
If l, m, n are the direction cosines and a, b, c are the direction ratios of a line then
If a line makes angles 90∘, 135∘, 45∘ with the x, y and z – axes respectively, find its direction cosines.
In the vector form, equation of a plane which is at a distance d from the origin, and is the unit vector normal to the plane through the origin is
Determine the direction cosines of the normal to the plane and the distance from the origin. Plane x + y + z = 1
In the following case, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them. 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0
|
204 videos|290 docs|139 tests
|