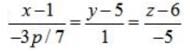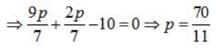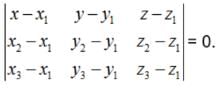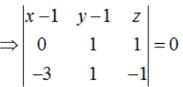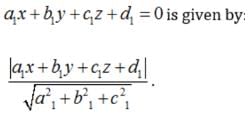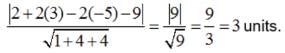Test: Three Dimensional Geometry- 2 - JEE MCQ
25 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Three Dimensional Geometry- 2
Skew lines are lines in different planes which are
If a line has the direction ratios – 18, 12, – 4, then what are its direction cosines ?
Equation of a plane which is at a distance d from the origin and the direction cosines of the normal to the plane are l, m, n is.
Find the vector equation of a plane which is at a distance of 7 units from the origin and normal to the vector
In the following case, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them. 2x – y + 3z – 1 = 0 and 2x – y + 3z + 3 = 0
Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector
The equation of a plane through a point whose position vector is perpendicular to the vector
. is
In the following case, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them. 4x + 8y + z – 8 = 0 and y + z – 4 = 0
If l1, m1, n1 and l2, m2, n2 are the direction cosines of two lines; and θ is the acute angle between the two lines; then
Find the equation of the line in cartesian form that passes through the point with position vector and is in the direction
Equation of a plane passing through three non collinear points (x1, y1, z1),(x2, y2, z2) and (x3, y3, z3) is
Find the distance of the point (0, 0, 0) from the plane 3x – 4y + 12 z = 3
If a1, b1, c1 and a2, b2, c2 are the direction ratios of two lines and θ is the acute angle between the two lines; then
Find the equation of the line in cartesian form that passes through the point (– 2, 4, – 5) and parallel to the line given by
Vector equation of a plane that contains three non collinear points having position vectors
The vector and cartesian equations of the planes that passes through the point (1, 0, – 2) and the normal to the plane is
Find the distance of the point (3, – 2, 1) from the plane 2x – y + 2z + 3 = 0
Vector equation of a line that passes through the given point whose position vector is and parallel to a given vector
is
Find the values of p so that the lines are at right angles.
Vector equation of a plane that passes through the intersection of planes expressed in terms of a non – zero constant λ is
Find the equations of the planes that passes through three points (1, 1, 0), (1, 2, 1), (– 2, 2, – 1)
Find the distance of the point (2, 3, – 5) from the plane x + 2y – 2z = 9
|
204 videos|290 docs|139 tests
|


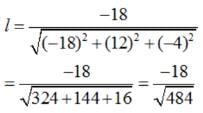
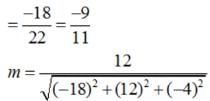
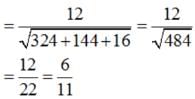
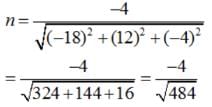
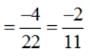

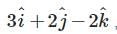 Let vector
Let vector  and vector
and vector 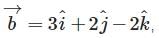
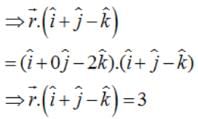
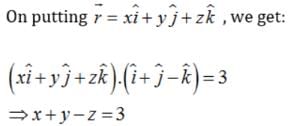
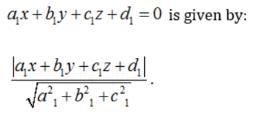

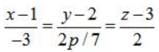 and
and