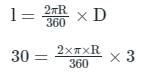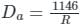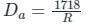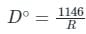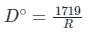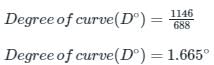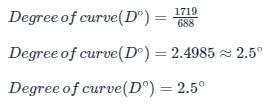Test: Curves - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Curves
If the radius of curve is 380m, what is its degree designation on 20m arc?
Determine the radius of curve if it is designated as 3° curve on a 30m arc.
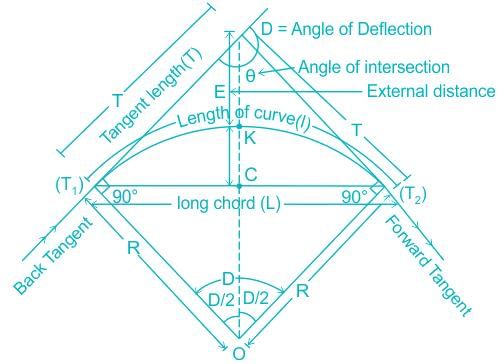
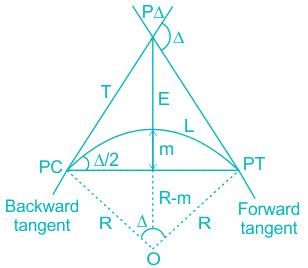
Two straight lines deflect through an angle of 60°, the radius of a curve joining the two straight lines is 600 m. The length of the long chord and mid ordinate (in m) of the curve respectively are
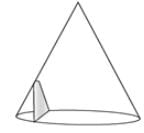
Figure below represents a section (shaded) obtained due to intersection by a plane that is parallel to the axes of the cones, what it the section called?
The degree of the curve is an angle subtended at the centre by a chord of length ________ and the degree of a curve with radius 688 m will be equal to _________.
The difference in length between the arc and the subtended chord on the earth's surface is taken as 500mm in: