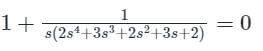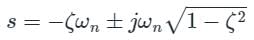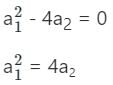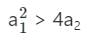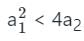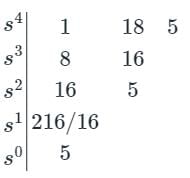Test: Routh-Hurwitz Stability - Electrical Engineering (EE) MCQ
15 Questions MCQ Test - Test: Routh-Hurwitz Stability
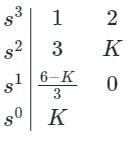
The characteristic equation of given system is 6s + K = 0. Determined the range of K for which the system to be stable.
The characteristic equation of a linear time-invariant (LTI) system is given by Δ(s) = s4 + 3s3 + 3s2 + s + k = 0. The system is BIBO stable if
The characteristic equation of a feedback system is s3 + Ks2 + 5s + 10 = 0. For a stable system, the value of K should not be less than
A closed loop system has the characteristic equation given by s3 + Ks2 + (K + 2)s + 3 = 0. For this system to be stable, which one of the following conditions should be satisfied?
What is the stability of the system s3 + s2 + s + 4 = 0 using Hurwitz criteria?
The characteristic polynomial of a linear system is given as s4 + 3s3 + 5s2 + 6s + K + 10 = 0. What should be the condition on K so that the system is stable?
Given the following polynomial equation
s3 + 5.5s2 + 8.5s + 3 = 0
the number of roots of the polynomial, which have real parts strictly less than −1, is ________
The number of roots of s3 + 5s2 + 7s + 3 = 0 in the left half of the s-plane is
In the formation of Routh-Hurwitz array for a polynomial, all the elements of a row have zero values. This premature termination of the array indicates the presence of
1. a pair of real roots with opposite sign
2. complex conjugate roots on the imaginary axis
3. a pair of complex conjugate roots with opposite real parts
Which of the above statements are correct?
Which of the following is the correct comment on stability based on unknown k for the feedback system with characteristic s4 + 2ks3 + s2 + 5s + 5 = 0?
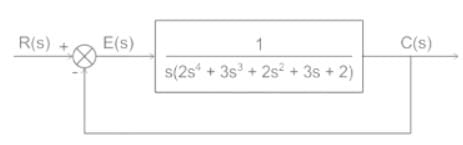
Find the number of poles in the right-half plane (RHP) for the system as shown. Is the system stable?
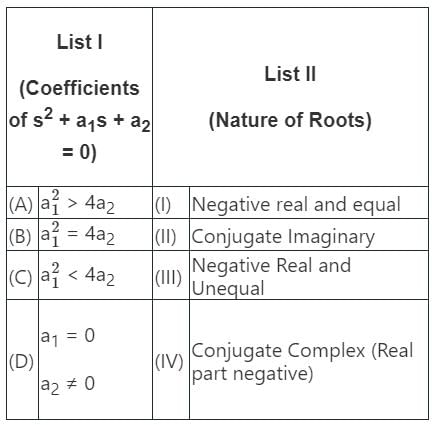
Match List I with List II:
Choose the correct answer from the options given below:
Find the range of k for stable operation if H(s) = 1 and G(s) 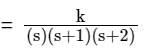
According to Hurwitz criterion, the characteristic equation
s4 + 8s3 + 18s2 + 16s + 5 = 0 is


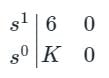


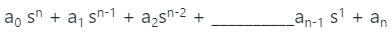

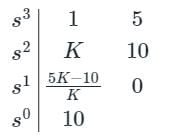
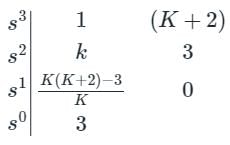

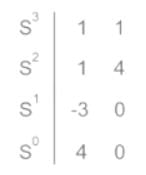
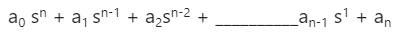

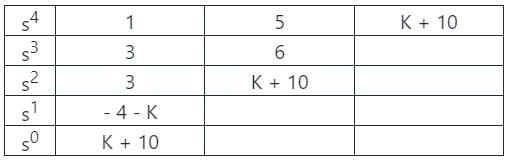
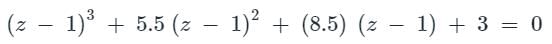

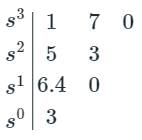
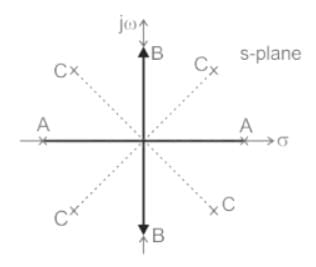
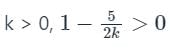
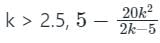 gives negative values.
gives negative values.