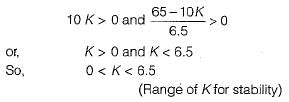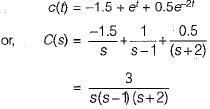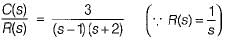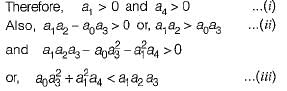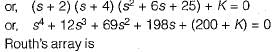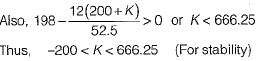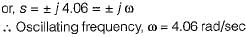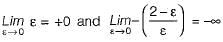Test: Stability Analysis of Linear Control Systems - 1 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Stability Analysis of Linear Control Systems - 1
The presence of non-linearities in a control system tends to introduce
Which one of the following is not a property of the Liapunov function?
The number of sign changes in the Routh’s array indicates the number of roots lying in the
Assertion (A): A system is said to be stable if the impulse response approaches zero for sufficiently large time.
Reason (R): If the impulse response approaches infinity for sufficiently large time, the system is said to be unstable
The open loop transfer function of a unity feedback system is 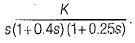
What is the range of value of K so that the closed loop system is absolutely stable?
Assertion (A): If the system is stable we can determine the relative stability by the settling time of the system.
Reason (R): If the settling time is less than that of the other system then the system is said to be relatively more stable.
If the unit step response of a system is given by c(t) = -1.5 + et + 0.5e-2f, then the system will be
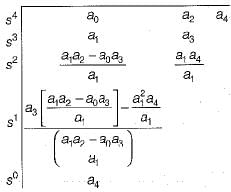
The characteristic equation of a servo system is given by
a0s4 + a1s3 + a2s2 + a3s + a4 = 0
Now, consider the following conditions required to be satisfied by the coefficient of the above characteristic equation for the system to be stable:
1. a1 > 0 and a4 > 0
2. a1 < 0 and a4 > 0
3. a1a2< a0a3
4. a1a2 > a0a3
5. 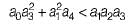
6. 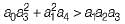
Which of the above conditions holds true for the given system to be stable?
The open loop transfer function of a unity feedback control system is given by
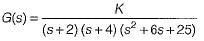
The oscillating frequency of the given system is
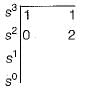
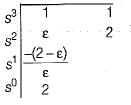
The characteristic equation of a system is given by s3 + s + 2 - 0.
What are the number of roots in the right half s-plane and on the jω-axis respectively?