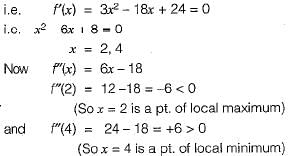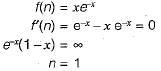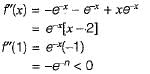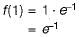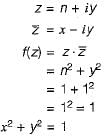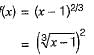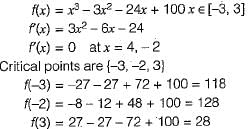Engineering Mathematics Exam > Engineering Mathematics Tests > Calculus > Test: Calculus- 2 - Engineering Mathematics MCQ
Test: Calculus- 2 - Engineering Mathematics MCQ
Test Description
15 Questions MCQ Test Calculus - Test: Calculus- 2
Test: Calculus- 2 for Engineering Mathematics 2025 is part of Calculus preparation. The Test: Calculus- 2 questions and answers have been
prepared according to the Engineering Mathematics exam syllabus.The Test: Calculus- 2 MCQs are made for Engineering Mathematics 2025 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Calculus- 2 below.
Solutions of Test: Calculus- 2 questions in English are available as part of our Calculus for Engineering Mathematics & Test: Calculus- 2 solutions in
Hindi for Calculus course. Download more important topics, notes, lectures and mock
test series for Engineering Mathematics Exam by signing up for free. Attempt Test: Calculus- 2 | 15 questions in 45 minutes | Mock test for Engineering Mathematics preparation | Free important questions MCQ to study Calculus for Engineering Mathematics Exam | Download free PDF with solutions
Test: Calculus- 2 - Question 1
What is the maximum value of the function f(x) = 2x2 - 2x + 6 in the interval [0, 2]?
Detailed Solution for Test: Calculus- 2 - Question 1
Detailed Solution for Test: Calculus- 2 - Question 2
Test: Calculus- 2 - Question 3
If f(x) is defined as follows, what is the minimum value of f{x) for x ∈ (0, 2]?
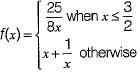
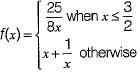
Detailed Solution for Test: Calculus- 2 - Question 3
Test: Calculus- 2 - Question 4
A point on a curve is said to be an extremum if it is a local minimum or a local maximum. The number of distinct extrema for the curve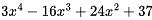 is
is
Detailed Solution for Test: Calculus- 2 - Question 4
Detailed Solution for Test: Calculus- 2 - Question 5
Detailed Solution for Test: Calculus- 2 - Question 6
Detailed Solution for Test: Calculus- 2 - Question 7
Test: Calculus- 2 - Question 8
Consider function f(x) = (x2- 4)2 where x is a real number. Then the function has
Detailed Solution for Test: Calculus- 2 - Question 8
Detailed Solution for Test: Calculus- 2 - Question 9
Detailed Solution for Test: Calculus- 2 - Question 10
Detailed Solution for Test: Calculus- 2 - Question 11
Test: Calculus- 2 - Question 12
Let f(x) = x e-x. The maximum value of the funntion in the interval (0, ∝) is
Detailed Solution for Test: Calculus- 2 - Question 12
Test: Calculus- 2 - Question 13
Minimum of the real valued function f(x) = (x-1)2/3 occurs at x equal to
Detailed Solution for Test: Calculus- 2 - Question 13
Test: Calculus- 2 - Question 14
The minimum value of the function f(x) = x3-3x2 - 24x + 100 in the interval [-3, 3] is
Detailed Solution for Test: Calculus- 2 - Question 14
Test: Calculus- 2 - Question 15
If a continuous function f(x) does not have a root in the interval [a, b], then which one of the following statements is TRUE?
Detailed Solution for Test: Calculus- 2 - Question 15
|
9 docs|20 tests
|
Information about Test: Calculus- 2 Page
In this test you can find the Exam questions for Test: Calculus- 2 solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Calculus- 2, EduRev gives you an ample number of Online tests for practice


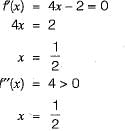
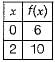
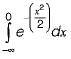
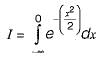
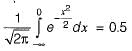
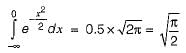

 the function has the value
the function has the value 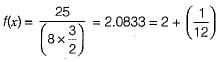
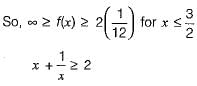
 this function we get the minimum of this function which is
this function we get the minimum of this function which is 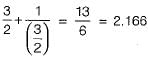
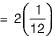 which is option (b).
which is option (b).
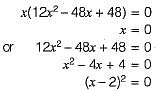
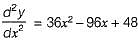
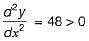
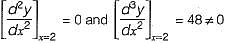
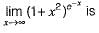

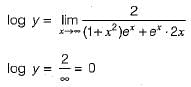
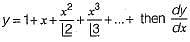 at x=0 ais equal to
at x=0 ais equal to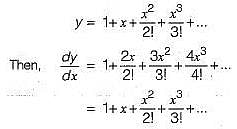
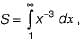 then S has the value
then S has the value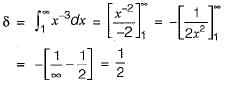
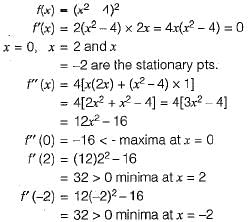
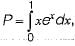 is equal to
is equal to
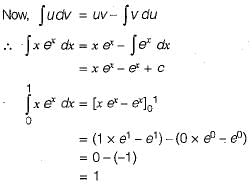
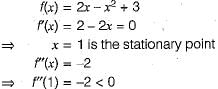
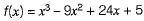 in the interval [1, 6] is
in the interval [1, 6] is