Test: Probability & Statistics- 1 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Probability & Statistics- 1
A fair dice is rolled twice. The probability that an odd number will follow an even number is
Three companies X, Y and Z supply computers to a university. The percentage of computers supplied by them and the probability of those being defective are tabulated below
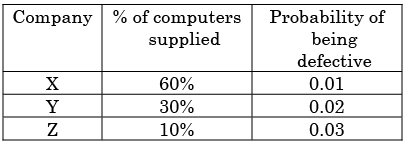
Given that a computer is defective, the probability that it was supplied by Y is
An examination consists of two papers, Paper 1 and Paper 2. The probability of failing in Paper 1 is 0.3 and that in Paper 2 is 0.2. Given that a student has failed in Paper 2, the probability of failing in Paper 1 is 0.6. The probability of a student failing in both the papers is
A fair coin is tossed 10 times. What is the probability that ONLY the first two tosses will yield heads?
Consider the continuous random variable with probability density function
The standard deviation of the random variables is
The probability that two friends share the same birth-month is
A box contains 5 black balls and 3 red balls. A total of three balls are picked from the box one after another, without replacing them back. The probability of getting two black balls and one red ball is
Two dice are thrown. What is the probability that is the sum of the numbers on the two dice is eight?
Arrivals at a telephone booth are considered to be poison, with an average time of 10 minutes between successive arrivals. The length of a phone call is distributes exponentially with mean 3 minutes. The probability that an arrival does not have to wait before service is
A box contains 5 black and 5 red balls. Two balls are randomly picked one after another from the box, without replacement. The probability for both balls being red is
A lot has 10% defective items. Ten items are chosen randomly from this lot. The probability that exactly 2 of the chosen items are defective is
A box contains 20 defective items and 80 non-defective items. If two items are selected at random without replacement, what will be the probability that both items are defective?
If three coins are tossed simultaneously, the probability of getting at least one head is
If 20 per cent managers are technocrats, the probability that a random committee of 5 managers consists of exactly 2 technocrats is
Four arbitrary point (x1,y1), (x2,y2), (x3,y3), (x4,y4), are given in the x, y – plane Using the method of least squares, if, regressing y upon x gives the fitted line y = ax + b; and regressing y upon x given the fitted line y = ax + b; and regressing x upon y gives the fitted line x = cy + d then
Chebyshev’s inequality states that the probability of a “Six Sigma” event is less than :
Three values of x and y are to be fitted in a straight line in the form y = a + bx by the method of least squares. GivenΣx = 6, Σy = 21, Σx2 = 14 and Σxy = 46, the values of a and b are respectively.
A box contains 10 screws, 3 of which are defective. Two screws are drawn at random with replacement. The probability that none of the two screws is defective will be
Which one of the following statements is NOT true?
If the standard deviation of the spot speed of vehicles in a highway is 8.8 kmph and the mean speed of the vehicles is 33 kmph, the coefficient of variation in speed is
|
55 docs|215 tests
|
|
55 docs|215 tests
|





















