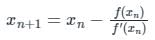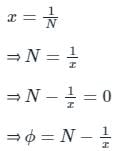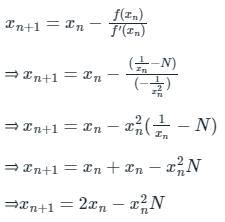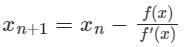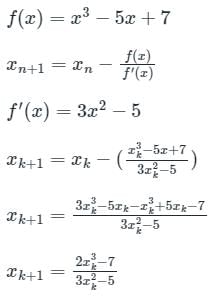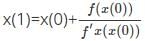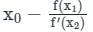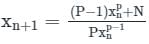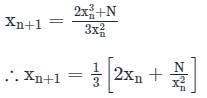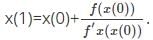Test: Newton Raphson Method - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Newton Raphson Method
The value of y’/x’ in terms of the angle 0 is given by ______
The Newton-Raphson method is to be used to determine the reciprocal of the number x = 4. If we start with the initial guess 0.20 then after the first iteration the reciprocal is
Starting with x = 1, the solution of the equation x3 + x = 1, after two iterations of newton raphson’s method (up to two decimal places) is
The iterative formula to find the root of the equation f(x) = x3 - 5x + 7 = 0 by the Newton Raphson method is ______.
Newton raphson method is to be used to find root of equation 3x – ex + sinx = 0. If the initial trial value of the roots is taken as 0.333, the next approximation for the root would be
The equation f(x) is given as x2-4=0. Considering the initial approximation at x = 6 then the value of x1 is given as ____________
The iteration step in order to solve for the cube roots of a given number Nusing the Newton- Raphson’s method is
The root of the function f(x) = x3 + x – 1 obtained after first iteration on application of newton raphson scheme using an initial guess of xo = 1 is
For decreasing the number of iterations in Newton Raphson method: