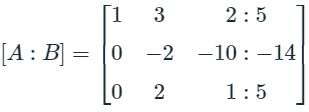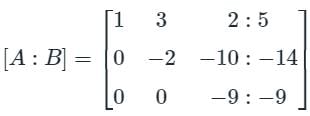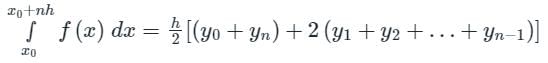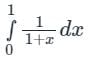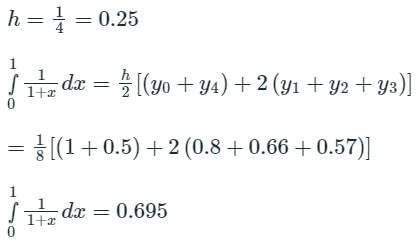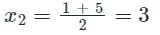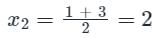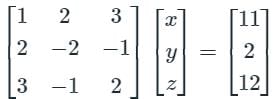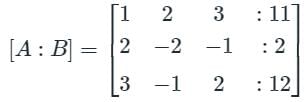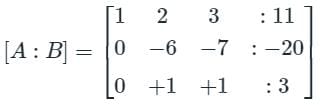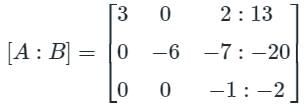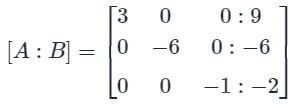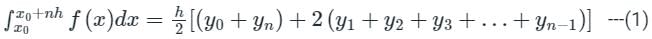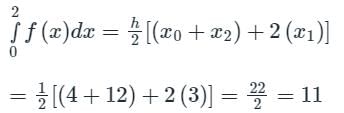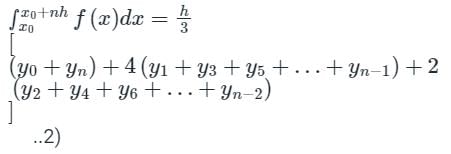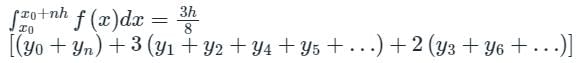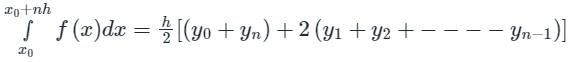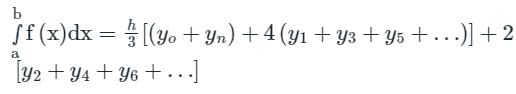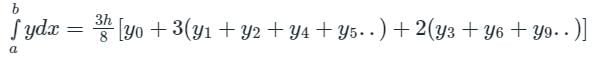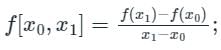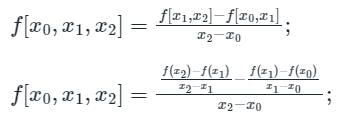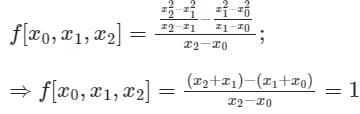Test: Numerical Methods - Grade 12 MCQ
10 Questions MCQ Test - Test: Numerical Methods
Find the difference between the sum of (x + y + z) and the Trace upper triangular matrix formed by using the gauss elimination method.
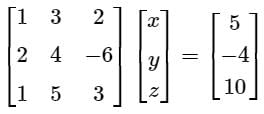
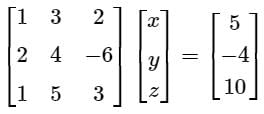
If dy/dx = x - y2 and y(0) = 1, then y(0.1) correct upto two decimal places (approx.) is:
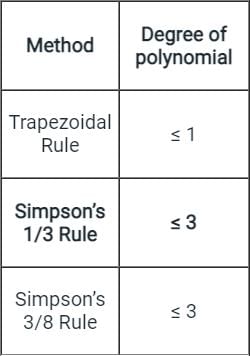
Which order of Polynomials can best be integrated using Trapezoidal Rules?
Considering four subintervals, the value of 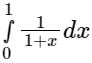 by Trapezoidal rule is:
by Trapezoidal rule is:
The bisection method is applied to compute a zero of the function f(x) = x4 – x3 – x2 – 4 in the interval [1, 9]. The method converges to a solution after _______ iterations.
Find the sum of the value of x, y, & z by using gauss jordan method.
3x - y + 2z = 12
x + 2y + 3z = 11
2x - 2y - z = 2
In which of the following categories can we put Bisection method?
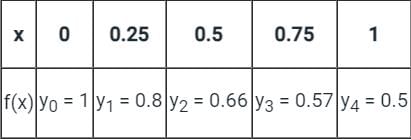
Consider the below data:

The value of 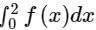 by Trapezoidal rule will be:
by Trapezoidal rule will be:
Trapezoidal Rule gives exact value of the integral when the integrand is a
If f(x) = x2, then the second order divided difference for the points x0, x1, x2 will be: