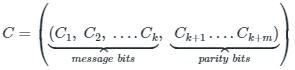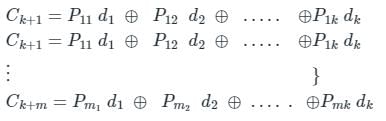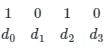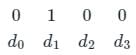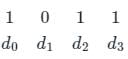Test: Hamming codes - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test Communication System - Test: Hamming codes
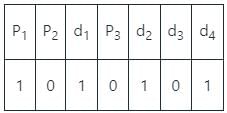
The representation of 4 bit code 1101 into 7 bit, even parity Hamming code is
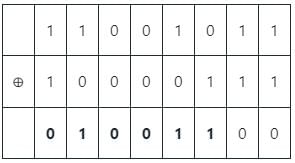
What is the hamming distance between the codes '11001011' and ‘10000111'
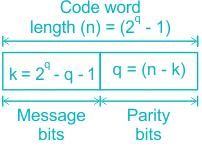
Which of the following codes uses a number of parity bits located at certain positions in the codeword and uses the relations between redundancy bits and the data bits?
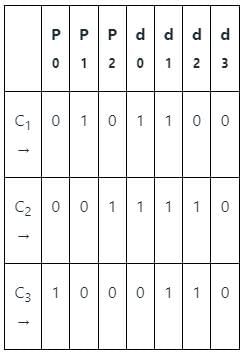
If one of the code words of a Hamming (7, 4) code is 0001011, which of the following cannot be the valid codeword in the same group?
For a linear block code, it is known that the code can detect 2 error and can correct only 1 error. The minimum hamming distance for the code is ________.
The final code after encoding data bits 1101 into 7-bit even parity Hamming Code is
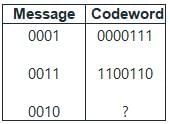
A linear Hamming code is used to map 4-bit messages to 7-bit code words. The encoder mapping is linear. If the message 0001 is mapped to the code word 0000111, and the message 0011 is mapped to the code word 1100110, then the message 0010 is mapped to
A digital transmission system uses a (7, 4) systematic linear Hamming code for transmitting data over a noisy channel. If three of the message-codeword pairs in this code (mi ; ci), where ci is the codeword corresponding to the ith message mi, are known to be (1 1 0 0 ; 0 1 0 1 1 0 0), (1 1 1 0 ; 0 0 1 1 1 1 0) and (0 1 1 0 ; 1 0 0 0 1 1 0), then which of the following is a valid codeword in this code?
Consider a binary channel code in which each code word has a fixed length of 5 bits. The Hamming distance between any pair of distinct code words in this code is at least 2. The maximum number of code words such a code can contain is ________.
|
13 videos|39 docs|30 tests
|