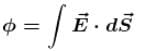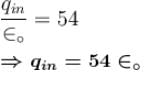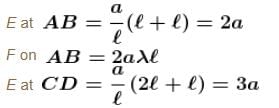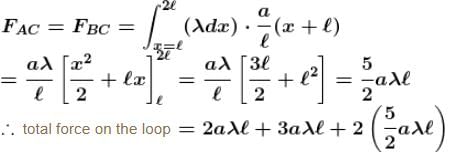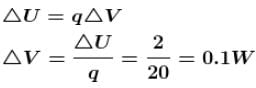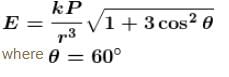Electrostatics NAT Level - 1 - IIT JAM MCQ
10 Questions MCQ Test - Electrostatics NAT Level - 1
A mercury drop of water has potential V on its surface. 1000 such drops combine to form a new drop. Find the potential (in Volts) on the surface of the new drop.
If the charge in a conductor is 16C and the area of cross section is 4m2. Calculate the electric flux density.
The number of electrons to be put on spherical conductor of radius 0.1m, to produce an electric field of 0.036N/C just above the surface is 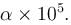 Find the value of α
Find the value of α
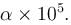 Find the value of α
Find the value of αAt distance of 5cm and 10cm outwards from the surface of a uniformly charged solid sphere, the potentials are 100V and 75V respectively. Then charge on the sphere is 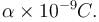 Find the Value of α.
Find the Value of α.
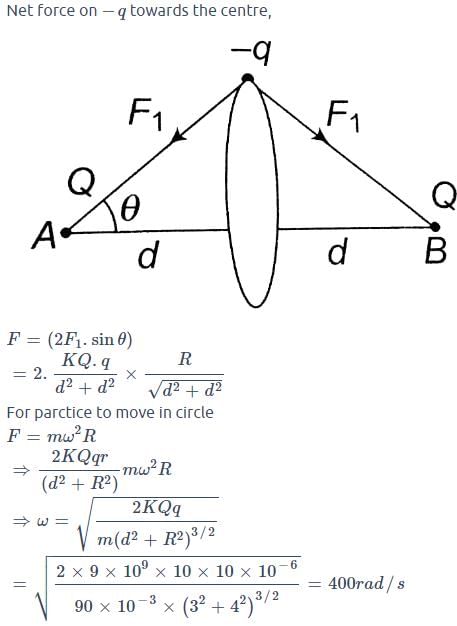
Two positive point charges each of magnitude 10C are fixed at positions A and B at a separation 2d = 6m. A negatively charged particle of mass m = 90gm and charge of magnitude 10 × 10–5C is revolving in a circular path of radius 4m in the plane perpendicular to the line AB and bisecting the line AB. Neglect the effect of gravity. If the angular velocity of the particle is 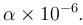 Then the value of α (in rad/sec) is :
Then the value of α (in rad/sec) is :

Eight point charges (can be assumed as small sphere uniformly charged and their centres at the corner of the cube) having values q each are fixed at vertices of a cube. The electric flux through square surface ABCD of the cube is 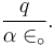 Find the value of α
Find the value of α

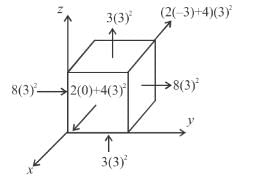
Figure given, shows a closed Gaussian surface in the shape of a cube of edge length 3.0m. There exists an electric field given by  where x is in metres, in the region in which it lies. The net charge in coulombs enclosed by the cube is equal to α∈0. Find the value of α.
where x is in metres, in the region in which it lies. The net charge in coulombs enclosed by the cube is equal to α∈0. Find the value of α.
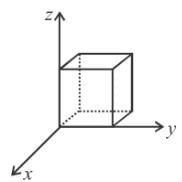
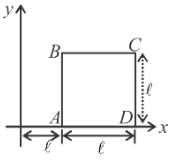
A square loop of side ℓ having uniform linear charge density λ is placed in xy plane as shown in the figure. There is a non-uniform electric field  where a is a constant. Then resultant electric force on the loop if ℓ = 10 cm, a = 2N/C and charge density λ = 2μC/m is
where a is a constant. Then resultant electric force on the loop if ℓ = 10 cm, a = 2N/C and charge density λ = 2μC/m is 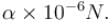 Find the value of α.
Find the value of α.
On moving a charge of 20coulombs by 2cm, 2J of work is done, then the potential difference (in Volts) between the points is :
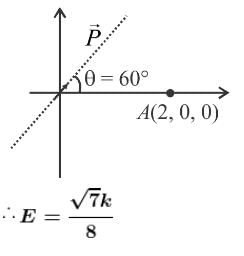
The magnitude of electric field intensity at point (2, 0, 0) due to a dipole moment,  kept at origin is αk [where k = 1/π ∈0]. Find the value of α.
kept at origin is αk [where k = 1/π ∈0]. Find the value of α.


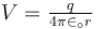

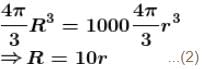
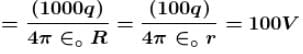


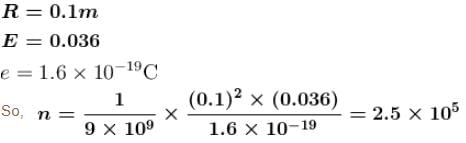
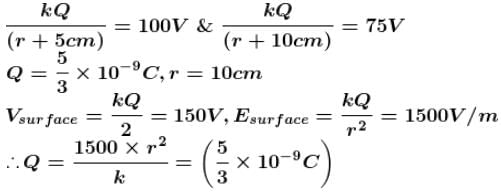

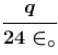 each.
each.