UGEE SUPR Mock Test- 4 - JEE MCQ
30 Questions MCQ Test - UGEE SUPR Mock Test- 4
In potentiometer experiment, null point is obtained at a particular point for a cell on potentiometer wire x cm long. If the length of the potentiometer wire is increased without changing the cell, the balancing length will (Driving source is not changed)
An iron rod is placed parallel to magnetic field of intensity 2000 Am-1. The magnetic flux through the rod is 6 × 10-4 Wb and its cross-sectional area is 3 cm2. The magnetic permeability of the rod in Wb A-1 m-1 is
An electron of mass m has de-Broglie wavelength λ when accelerated through potential difference V. When proton of mass M, is accelerated through potential difference 9 V, the de-Broglie wavelength associated with it will be (Assume that wavelength is determined at low voltage)
Interference fringes are produced on a screen by using two light sources of intensities I and 9I. The phase difference between the beams is π/2 at point P and π at point Q on the screen. The difference between the resultant intensities at point P and Q is
From Brewster's law, except for polished metallic surfaces, the polarizing angle:
Two particles X and Y having equal charges after being accelerated through the same potential difference enter a region of uniform magnetic field and describe circular paths of radii r1 and r2 respectively. The ratio of the mass of X to that of Y is:
The magnetic field (B) inside a long solenoid having n turns per unit length and carrying current/when iron core is kept in it is (μ₀ = permeability of vacuum, x = magnetic susceptibility)
In an oscillator, for sustained oscillations, Barkhausen criterion is Aβ equal to (A = voltage gain without feedback and β = feedback factor)
Light of wavelength λ which is less than threshold wavelength is incident on a photosensitive material. If incident wavelength is decreased so that emitted photoelectrons are moving with same velocity, then stopping potential will
A ray of light travelling through rarer medium is incident at very small angle i on a glass slab and after refraction its velocity is reduced by 20%. The angle of deviation is:
The maximum frequency of transmitted radio waves above which the radio waves are no longer reflected back by ionosphere is (N = maximum electron density of Ionosphere, g = acceleration due to gravity)
If a = î + ĵ - 2k̂, b = 2î - ĵ + k̂, and c = 3î - k̂ and 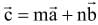 , then m + n is equal to
, then m + n is equal to
If the probability density function of a random variable X is given as:
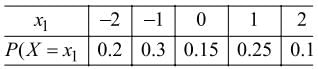
The cumulative distribution function is defined by:
F(x) = P(X ≤ x)
then F(0) is equal to
The length of the diameter of the circle which cuts three circles
x² + y² - x - y - 14 = 0
x² + y² + 3x - 5y - 10 = 0
x² + y² - 2x + 3y - 27 = 0
orthogonally, is
The number of values of c such that the line y = 4x + c touches the curve x²/4 + y² = 1 is
The vertices of a triangle are (6, 0), (0, 6) and (6, 6). The distance between its circumcentre and centroid is
2 g of a radioactive sample having half-life of 15 days was synthesised on 1st Jan 2009. The amount of the sample left behind on 1st March, 2009 (including both the days) is
For a chemical reaction A → B, the rate of the reaction is 2 × 10-3 mol dm-3 s-1, when the initial concentration is 0.05 mol dm-3. The rate of the same reaction is 1.6 × 10-2 mol dm-3 s-1 when the initial concentration is 0.1 mol dm-3.The order of the reaction is
For the decomposition of a compound AB at 600 K, the following data were obtained.

The order for the decomposition of AB is
The rate equation for a reaction A → B is r = k[A]⁰. If the initial concentration of the reactant is a mol dm-3, the half-life period of the reaction is
30 cc of M/3 HCl, 20 cc of M/2 HNO3 and 40 cc of M/4 NaOH solutions are mixed and the volume was made up to 1 dm3. The pH of the resulting solution is
An aqueous solution containing 6.5 g of NaCl of 90% purity was subjected to electrolysis. After the complete electrolysis, the solution was evaporated to get solid NaOH. The volume of 1 M acetic acid required to neutralize NaOH obtained above is


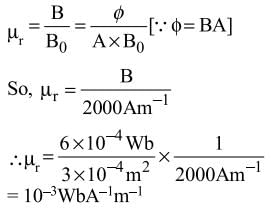

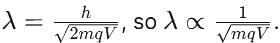
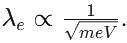
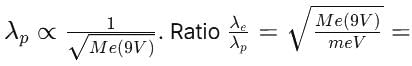
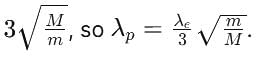
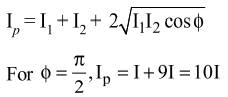
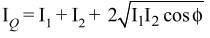
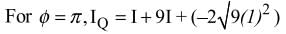
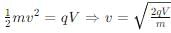
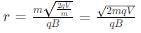
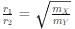
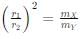

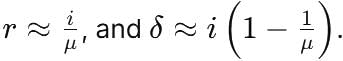
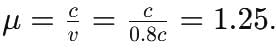
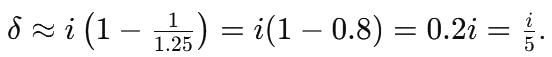
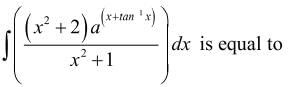
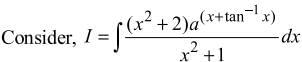
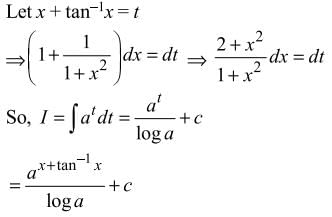
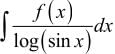 = log[log sin x] + c, then f(x) is equal to
= log[log sin x] + c, then f(x) is equal to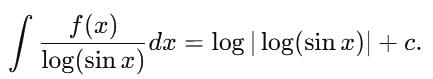
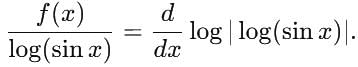
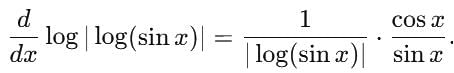
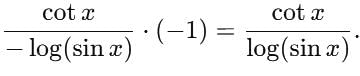
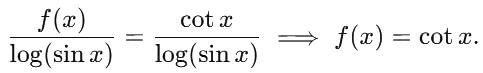
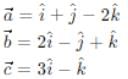
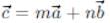
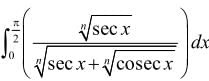 is equal to
is equal to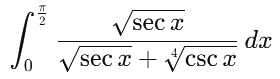
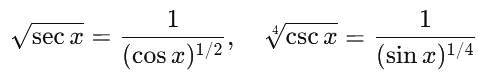
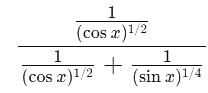
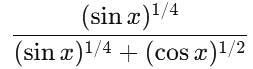
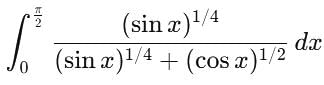

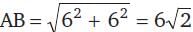
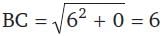

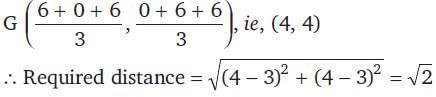
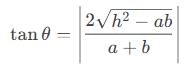

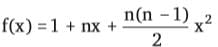
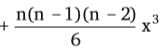 + ... + xn, then f''(1) is equal to
+ ... + xn, then f''(1) is equal to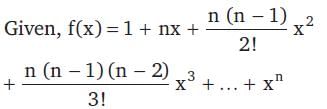
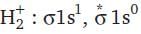
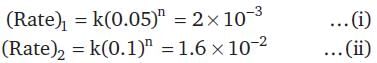


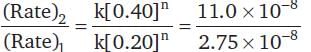
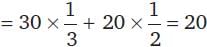
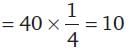
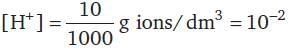
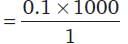 = 100 cm3
= 100 cm3















