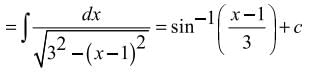UGEE SUPR Mock Test- 6 - JEE MCQ
30 Questions MCQ Test - UGEE SUPR Mock Test- 6
At how many points between the interval (-∞, ∞) is the function f(x) = sin x is not differentiable.
The radius of a right circular cylinder increases at the rate of 0.1 cm/min, and the height decreases at the rate of 0.2 cm/min. The rate of change of the volume of the cylinder, in cm³/min, when the radius is 2 cm and the height is 3 cm is
The equation y2 + 3 = 2(2x+y) represents a parabola with the vertex at
The conic represented by x = 2(cos t + sin t), y = 5(cos t − sin t) is
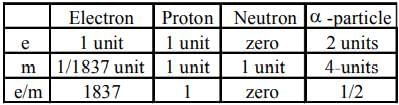
Arrange the following particles in increasing order of values of e/m ratio: electron (e), proton (p), neutron (n) and α-particle (α) -
For the reaction N2 + 3H2 → 2NH3
if 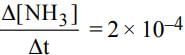 mol L−1 s−1, then value of
mol L−1 s−1, then value of 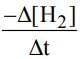 would be
would be
The value of Kc for the reaction:
A + 3B ⇌ 2C at 400∘C is 0.5. Calculate the value of Kp
The electrode potentials for
Cu²⁺(aq) + e⁻ → Cu⁺(aq)
and Cu⁺(aq) + e⁻ → Cu(s)
are +0.15 V and +0.50 V, respectively.
The value of E°Cu²⁺/Cu will be:
The wavelengths of two photons are 2000Å and 4000Å respectively. What is the ratio of their energies?
A far-sighted person can see clearly object beyond 100 cm distance. If he wants to see clearly an object at 40 cm distance, then the power of the lens he shall require is
A 20 cm long capillary tube is dipped in water. The water rises up to 8 cm. If the entire arrangement is put in a freely falling elevator the length of water column in the capillary tube will be ______ cm.
The work function of a metallic surface is 5.01 eV. Photoelectrons are emitted when light of wavelength 2000 Å falls on it. What is the minimum potential difference required to stop the fastest photoelectrons? (h = 4.14 × 10-15 eV·s)
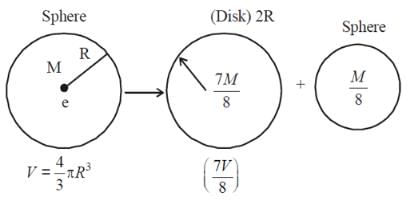
A solid sphere of mass M and radius R is divided into two unequal parts. The first part has a mass of 7M/8 and is converted into a uniform disc of radius 2R. The second part is converted into a uniform solid sphere. Let I1 be the moment of inertia of the new sphere about its axis. The ratio I1/I2 is 140/x. Find the value of x.
Note: I1 is the inertia of the disk & I2 is the inertia of the new sphere about the diameter.
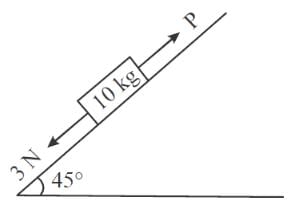
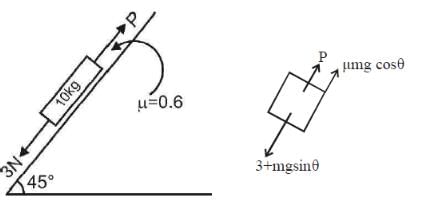
A block of mass 10 kg is kept on a rough inclined plane as shown in the figure. A force of 3 N is applied on the block. The coefficient of static friction between the plane and the block is 0.6. What should be the minimum value of force P (in newton), such that the block does not move downward? (Take g = 10 m/s2)
A plane electromagnetic wave of frequency 50 MHz travels in free space along the positive x-direction. At a particular point in space and time, 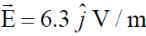 . The corresponding magnetic field
. The corresponding magnetic field 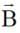 , at that point is
, at that point is 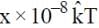 . Find the value of x.
. Find the value of x.
Two concentric coplanar circular loops made of wire, with resistance per unit length 10 Ω/m have diameters 0.2 m and 2 m. A time varying potential difference (4 + 2.5 t) volt is applied to the larger loop. Calculate the current (in A) in the smaller loop.
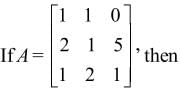
a11A21 + a12A22 + a13A23 is equal to
Note: axy represents element whereas Axy represents Cofactor matrix.
If Rolle's theorem for
f(x) = ex (sin x − cos x) is verified on [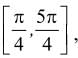 then the value of c is
then the value of c is
The approximate value of f(x) = x3 + 5x2 - 7x + 9at x = 1.1 is


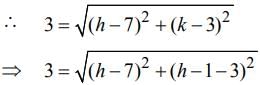 [using (i)]
[using (i)]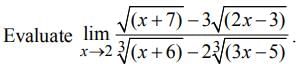
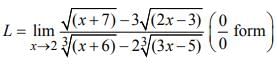
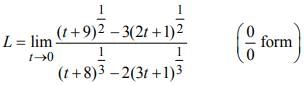
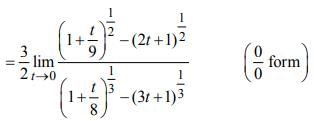
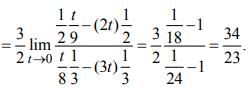

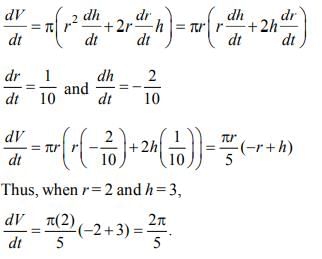
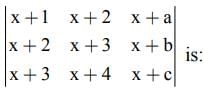
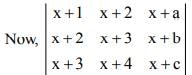
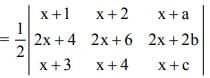
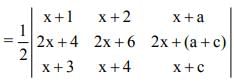
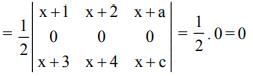
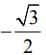 is
is 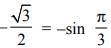
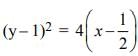 which is a parabola
which is a parabola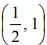 , axis along the line
, axis along the line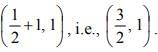



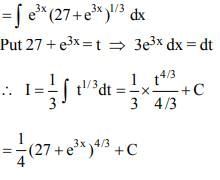
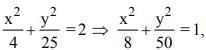 which is an ellipse.
which is an ellipse.
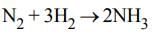
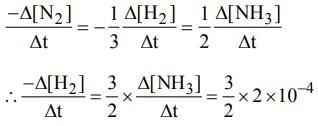
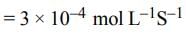

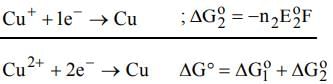
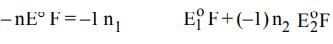
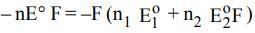
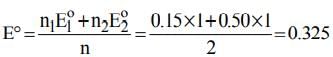
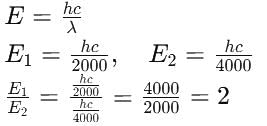
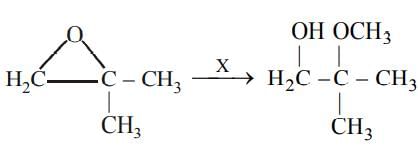
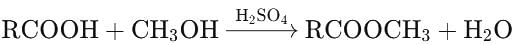
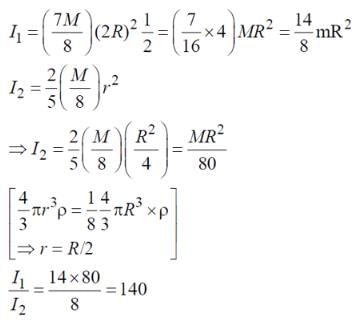
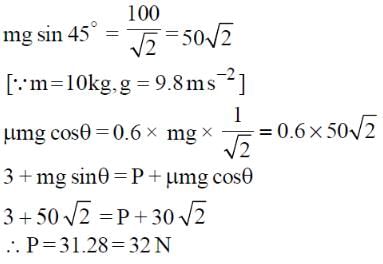
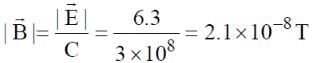
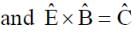
 [ ∵ EM wave travels along + (ve) x-direction]
[ ∵ EM wave travels along + (ve) x-direction]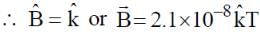

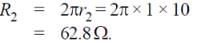
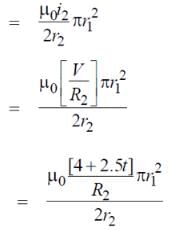
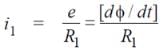
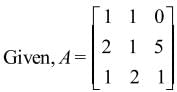
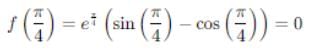
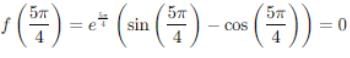
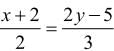 , z = -1 are
, z = -1 are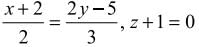
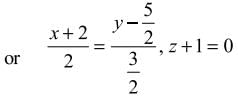
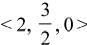
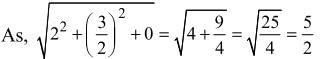
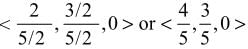
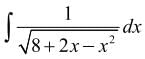 is equal to
is equal to