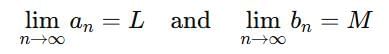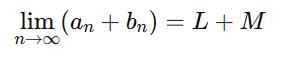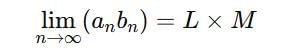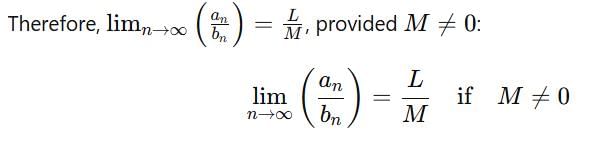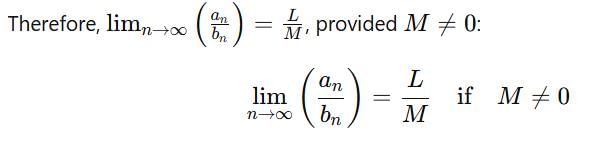Sequences And Series Of Real Numbers -4 - IIT JAM MCQ
20 Questions MCQ Test - Sequences And Series Of Real Numbers -4
Which amongst the following statements is true?
A Cauchy sequence is convergent, if it is a
If radius of convergence of series is 1, then radius of convergence of series
is…
If {xn} and {yn} are two convergent sequence such that xn < yn, 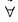 n ∈ N, then
n ∈ N, then
Let a = min{x2 + 2x + 3, x ∈ R} and 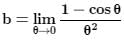 then the value of
then the value of 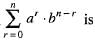
If for any e > 0, there exists a positive integer m such that I an - am | < e whenever n ≥ m . The sequence an > is called
A convergent sequence is a Cauchy sequence, if it is a
For the given Arithmetic progression find the position of first negative term? 50, 47, 44, 41,............
In the given AP series the term at position 11 would be? 5, 8, 11, 14, 17, 20.........50.
A sequence contains a convergent subsequence, if it is
Let {an}∞n=1 be a sequence converges to 0 and {bn}∞n=1 be a sequence that is bounded, then {anbn}∞n=1 is a sequence that
Which of the following sequences of functions is uniformly convergent on (0, 1)?
The sequence {xn}, where xn = nl/n, converge to
Let xn = 22n 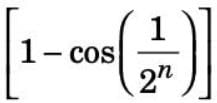 for all n ∈ N. Then the sequence {xn}
for all n ∈ N. Then the sequence {xn}


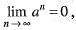 then
then

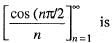
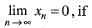
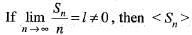


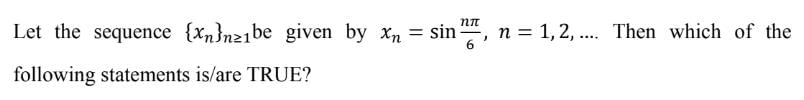




 are convergent, then
are convergent, then