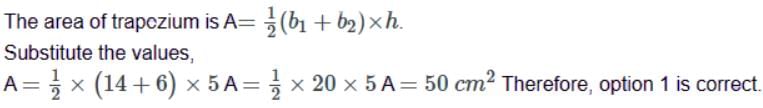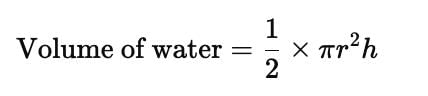Test: Mensuration- 1 - Class 8 MCQ
20 Questions MCQ Test Mathematics (Maths) Class 8 - Test: Mensuration- 1
Which of the following has the formula ½ (sum of parallel sides)×h
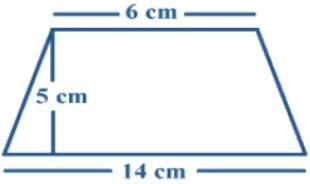
The length of parallel sides of trapezium is 14 cm and 6 cm and its height is 5 cm. Its area will be
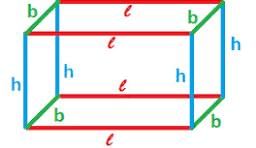
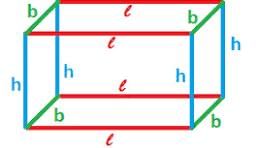
If a cuboidal box has height, length and width as 20 cm, 15 cm and 10 cm respectively. Then its total surface area is:
The height of a cuboid whose volume is 275 cm3 and base area is 25 cm2 is:
A glass in the form of a right circular cylinder is half full of water. Its base radius is 3 cm and height is 8 cm. The volume of water is
The height of a cylinder whose radius is 7 cm and the total surface area is 968 cm2 is:
The base radius and height of a right circular cylinder are 5 cm and 10 cm. Its total surface area is
The height of cuboid whose volume is 200 cm3 and base area is 20 cm2 is
If each edge of a cube is doubled, its surface are will increase
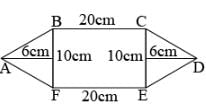
If the diagonals of rhombus are 6 cm & 8 cm, its area will be
If the base of rhombus of 7 cm and its altitude is 4 cm, its area will be
|
81 videos|415 docs|31 tests
|