Test: Stability Of Equilibrium Configurations - Mechanical Engineering MCQ
15 Questions MCQ Test Additional Study Material for Mechanical Engineering - Test: Stability Of Equilibrium Configurations
The main condition for the stability of equilibrium configuration is that the distance between various particles of the body does change.
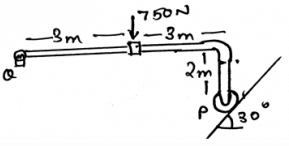
Determine the vertical components of the reaction on the beam caused by the pin at Q.
Which of the following is correct for stability of equilibrium configuration?
For stability of equilibrium configuration the net force acting on the body is zero.
For stability of equilibrium configuration the net moment acting on the body by various forces is zero.
The net force of the body is zero that means the force are not being applied to the body at all and hence the body has achieved stability.
Which of the following needs to zero for the stability of equilibrium configuration?
Determine the horizontal components of the reaction on the beam caused by the pin at Q. The force 60N is multiplied by 10 and then is applied.
Free body diagrams doesn’t play any role in making the calculations on the conditions of stability of equilibrium configuration.
The net moment of the body is zero that means the distance between the force and the rotational axis is zero thus the stability of equilibrium configuration.
If the resolved force for the stability of equilibrium configuration or the force which you get as the answer after solving the question is negative, then what does this implies?
If the body is in stability of equilibrium configuration, but it having a rotational curled ray shown in the free body diagram then:
If five forces are acting on the single particle and having an angle of 72˚ between each and are collinear, then:
For the conditions of the stability of equilibrium configuration of the body, i.e. the body only the external forces defines the equilibrium. Because the internal forces cancels out so not to be considered.
We need to apply vector math sometimes in the calculation of stability of equilibrium configurations. So the coordinate of the Force vector AB is A (2, 0, 2) and B (-2, 3.46, 3). It has a magnitude of 750N. Which is the best Cartesian representation of the vector AB?
|
1 videos|30 docs|57 tests
|
|
1 videos|30 docs|57 tests
|




















