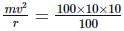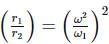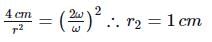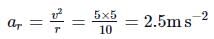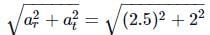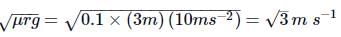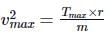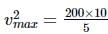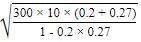Test: Circular Motion (NCERT) - NEET MCQ
10 Questions MCQ Test NCERTs at Fingertips: Textbooks, Tests & Solutions - Test: Circular Motion (NCERT)
A motor cyclist rides around the well with a round vertical wall and does not fall down while riding because
One end of a string of length I is connected to a particle of mass m and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed v, the net force on the particle directed towards the centre is (where T is the tension in the string)
The mass of a bicycle rider along with the bicycle is 100 kg. He wants to cross over a circular turn of radius 100 m with a speed o f 10 m s-1. If the coefficient of friction between the tyres and the road is 0.6, the frictional force required by the rider to cross the turn, is
A stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are
T1 and v1 denotes the tension and speed at the lowest point. T2 and v2 denotes corresponding values at the highest point.
A small object placed on a rotating horizontal turn table just slips when it is placed at a distance 4 cm from the axis of rotation. If the angular velocity of the turn-table is doubled, the object slips when its distance from the axis of rotation is
A particle is moving on a circular path of 10 m radius. At any instant of time, its speed is 5 m s-1 and the speed is increasing at a rate of 2 m s-1. The magnitude of net acceleration at this instant is
The coefficient of frictionbetween the tyres and the road is 0.1. The maximum speed with which a cyclist can take a circular turn of radius 3m without skidding it.(Take g = m s-2)
A stone of mass 5 kg is tied to a string of length 10 m is whirled round in a horizontal circle. Wha is the maximum speed with which the stone can be whirled around if the string can witbstand a maximum tension of 200 N.
In the question number 8, the maximum permissible speed to avoid slipping is
|
257 docs|234 tests
|